Лекция №7 минимизация функции

Правила алгебры логики применяют для преобразования исходных выражений к виду, удобному для их практической реализации. В этом случае логические функции задаются в виде таблицы истинности, в которой всем возможным значениям аргументов присваивается определенное значение функции.

Рассмотрим пример минимизации функции. Допустим логические переменные А,В,С принимают следующие значение, приведенные, в таблице, где “Y” логическая функция трех переменных (А, В, С).

A	B	C	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Эта функция принимает единичное значение при наборах переменных

_.

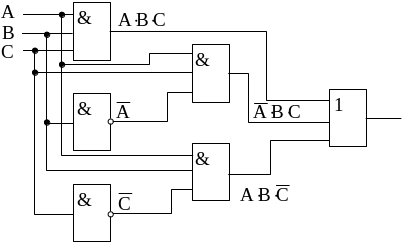
Рис. Минимизация функции

Для реализации полученной логической функции потребуются три трехходовые схемы И, одна трехходовая схема ИЛИ и два инвертора(НЕ), т. е. шесть логических элементов (микросхем).

Теперь, используя правила алгебры логики, преобразуем

исходное уравнение и схему реализации его к более удобному виду.

Преобразуем исходное уравнение

,

применяя правило 8, получим:

_.

Для преобразования выражения в скобках используем правило 17:

(*)

Очевидно, что полученное выражение значительно проще при реализации, чем исходное уравнение.

Сравним результат преобразования с исходным условием.

Сравнивая эти две схемы видно, что как технологичность реализации, так и экономическая выгодность варианта преобразования имеет неоспоримое преимущество.

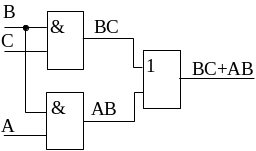
Рис. Минимизация функции

Применяя к преобразованной функции законы инверсии (18, 19) можно получить тот же результат, только на базе других элементов.

Допустим, для реализации преобразованной функции в наличии имеются только элементы И-НЕ.

Применим к функции (*) правила 9 и 19 и получим:

_. Функциональная схема полученного уравнения приведена ниже.

Рис. Минимизация функции

Таким образом, экономическая выгодность (более, чем в два раза) и надежность, которые обеспечиваются путем преобразования - минимизации логической функции очевидна.

Для минимизации логических функций обычно используется диаграмма или же, как принято называть, карта Карно.

Ниже приведены диаграммы Карно для трех переменных. Каждая клеточка диаграммы соответствует логическому произведению прямого или инверсионного значения переменных, присвоенных столбцу или строке, на пересечении которых она находится. Например, клетка № 0 находится на пересечении строки со значением переменной и столбца со значениями переменных и и соответствует произведению . В диаграммах (картах) Карно значения переменных присваиваются таким образом, чтобы соседние клетки по строкам и столбцам отличались между собой значениями только одной переменной. Клетки, находящиеся на границах одной строки или одного столбца, считаются соседними.

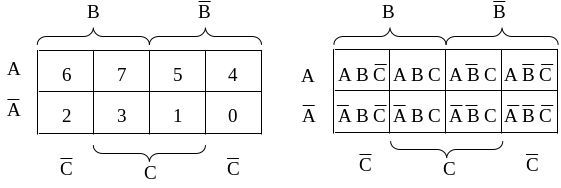
Для заполнения клеток 0-7 воспользуемся таблицей истинности 3-х переменных, приведенной ранее, где прямое значение логической переменной А, В, С соответствует 1, а инверсной - 0, где 0-7 - номера клеток, которые соответствуют последовательности значений логических переменных. Номера клеток соответствуют значениям логических переменных. Например, клетки 2, 3, соответственно (условно) пронумерованы согласно значению переменной “С”- 2 , 3С.

0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 -

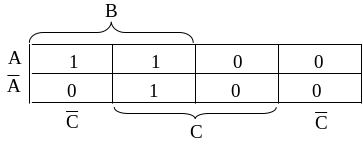
Пользуясь таблицей истинности 3-х переменных (см. выше), составим карту Карно, где в клетки записывают значения логических произведений из таблицы истинности.

КОНТРОЛЬНАЯ РАБОТА

Минимизировать заданную функцию с использованием законов алгебра логики:

Y= + + +