
- •Лекция №1 литература.
- •План лекции
- •Самостоятельная проработка
- •Введение
- •1. Назначение и краткий обзор развития схемотехники эвм(5 проблем)
- •2. Активны и пассивные элементы схемотехники
- •4. Понятие блок-схемы, функциональной и принципиальной схемы
- •5.Условные обозначения схемотехнических элементов
- •Лекция №2 План лекции.
- •3. Формы представления информации
- •4. Входной контроль
- •1 Краткий словарь схемотехники
- •2. Функциональная схема эвм и принцип ее работы
- •3. Формы представления информации
- •Лекция №3 план лекции
- •Функциональные узлы эвм
- •2 Формирование и преобразование сигналов
- •Дифференцирующие цепи
- •Оперативное запоминающее устройство
- •Устройство управления
- •Арифметическое устройство
- •Самостоятельная работа формирование и преобразование сигналов Дифференцирующие цепи
- •Интегрирующие цепи (иц)
- •Лекция №4 план лекции
- •Код. Кодирование. Способы кодирования
- •Формы представления чисел
- •3. Двоичное кодирование текстовой информации
- •4. Двоичное кодирование графической информации
- •2. Формы представления чисел
- •3. Двоичное кодирование текстовой информации
- •4. Кодирование графической информации
- •Изображения растровые векторные
- •Кодирование векторных изображений.
- •Лекция №5
- •5.1 Логическое отрицание не
- •5.2 Логическое умножение и
- •5.3 Логическая функция сложения или
- •5.4 Функция Шеффера
- •5.5 Стрелка Пирса
- •5.6 Исключающее или
- •5.7 Эквивалентность
- •5.8 Импликация
- •Лекция №6а план лекции
- •Этапы развития логики
- •Законы алгебры логики
- •Законы алгебры логики
- •Лекция №7 минимизация функции
- •Самостоятельная работа Минимизация логической функции
- •Лекция №8-9 план лекции
- •1.Принцип работы полупроводниковых устройств
- •2. Потенциальные системы схем эвм
- •Рассмотрим принцип работы транзистора
- •Инвертор
- •Транзисторная логика(самостоятельная работа)
- •Лекция №10 схемотехника транзисторно-транзисторнй логики (ттл)
- •Лекция №11
- •2. Схемотехника ис инжекционной логики--иил (и2л)
- •Схемотехника ис инжекционной логики и2л
- •Лекция 12
- •Схемотехника транзисторной логики со связанными эмиттерами(эстл).
- •2. Схемотехника ис на полевых транзисторах (пт)
- •Схемотехника ис на полевых транзисторах (пт)
- •Лекция №12а схемотехника цифровых элементов
- •9.1 Схемотехника триггерных схем
- •9.2 Асинхронный rs-триггер
- •Лекция №13
- •10.0 Основные динамические параметры интегральных схем потенциального типа
- •Самостоятельная работа Развитие схем потенциального типа
- •10.2 Таблица сравнения цифровых интегральных микросхем
- •Лекция №13а схемотехника цифровых элементов
- •9.1 Схемотехника триггерных схем
- •9.2 Асинхронный rs-триггер
- •Лекция №14
- •11.0 Регистры хранения и сдвига
- •11.1 Регистры сдвига на d-триггерах с параллельным выводом информации
- •Лекция №14а универсальные jk триггеры
- •9.7 Триггер Шмитта – (тл)
- •Лекция №15 универсальные регистры
- •Лекция №17(самотоятельно) кольцевой счетчик
- •12.3 Делители частоты
- •Лекция №18a синхронный (тактируемый) rs, d и т триггеры
- •Выходной сигнал q сохраняется до прихода очередного тактового импульса. Причем эта информация хранится в d-триггере, пока не придет следующий бит (0 или 1) информации. По сути это ячейка памяти.
- •Лекция №20 регистры хранения и сдвига
- •Регистры сдвига на d-триггерах с параллельным выводом информации
- •Лекция №21 план лекции
- •Реверсивные счетчики (рс)
- •Кольцевой счетчик
- •Делители частоты(Самостоятельно)
- •Лекция №23 преобразователи кодов
- •Лекция №24 дешифраторы decoder (dc)
- •Контрольная работа Используя таблицу истинности составить временные диаграммы дешифратора 2х4
- •Лекция №25
- •Пример сети с двумя типами мультиплексоров самостоятельная работа
- •Лекция №26 демультиплексоры
- •Лекция №27 сумматоры и алу
- •Контрольная работа
- •Лекция №28 сумматоры и алу
- •Лекция №29-30 схемотехника обслуживающих элементов Генераторы и формирователи импульсов
- •Формирователи импульсов
- •Лекция №28 схемотехника аналоговых и комбинированных узлов Операционные усилители(оу)
- •Лекция №31 схемотехника аналоговых и комбинированных узлов Операционные усилители(оу)
- •Лекция №32-33 компараторы и таймеры
- •Цифро-аналоговые и аналого-цифровые преобразователи
Законы алгебры логики
При рассмотрении законов алгебра логики А, В логические переменные, Еп источник , а Х- результат операции.
Правило 1.
![]()
Логическое произведение любого аргумента на 0=0. Это правило часто используется для выполнения процедуры “маскирования” входных переменных.
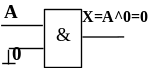
Правило 2.
![]()
Логическое произведение любого аргумента на 1 равно значению аргумента. Доказательства правил 1 и 2 можно получить подстановкой значений аргументов в таблицы истинности для логических функций И, ИЛИ.
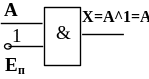
Правило 3.
Логическое произведение одних и тех же аргументов равно аргументу. В таблице истинности этому правилу соответствуют значения аргументов А=0, Х=0 и А=1 и Х=1.
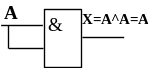
Правило 4.
Х=![]() .A=0
.A=0
Логическое произведение аргумента с его инверсией=0.

Правила 5, 6, 7 касаются логической суммы и аналогичны правилам для логических произведений.
5)
![]() 6)
6)
![]()

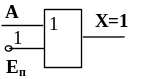
7)
![]() 8)
8)
![]()
![]()

Правило 9.
![]()
Двойная инверсия аргумента дает его истинное значение.
![]()
Правило 10.
![]()
Правило 11.
![]()
Правила 10, 11 аналогичны переместительному закону алгебры и указывают на возможность перемещения аргументов в логических функциях И, ИЛИ.
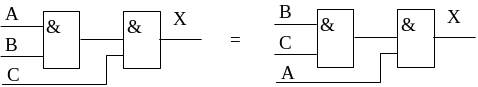
Правило 12.
![]()
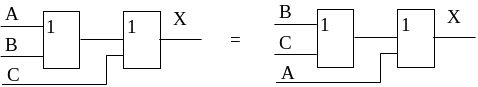
Правило 13.
![]()
Правила 12 и 13 аналогичны сочетательному закону алгебры и показывают, что аргументы логических функций И, ИЛИ можно группировать произвольно.
Правило 14.
![]()
Правило 15.
![]()
Правило 15 можно доказать при помощи составления и сравнения таблиц истинности для правой и левой частей каждой формулы, описывающей тот или иной закон.
Левая часть Правая часть
A |
B |
C |
BC |
A+(BC) |
A |
B |
C |
A+ B |
A+ C |
(A+ B) (A+ C) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Из таблиц видно, что результаты одинаковые и доказано тождество.
Правило 16.
![]()
Правило 17.
![]() =А+В
=А+В
Правила 16 и 17 применяют при преобразовании логических выражений.
Для доказательства правила 16 воспользуемся правилами 2 и 6:
![]()
для доказательства правила 17 воспользуемся правилом 15:
=(А+![]() ).(А+В)=А+В
).(А+В)=А+В
Правило 18.
![]()
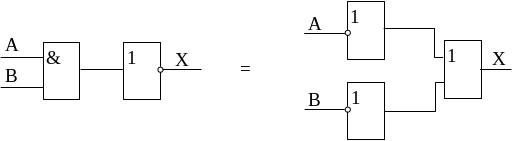
Правило 19.
![]()
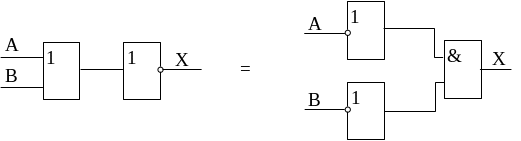
Правила 18 и 19 известны как правила ДЕ Моргана, или законы инверсии.
Чтобы убедиться в справедливости правил 16-19 воспользуемся методом доказательства при помощи таблиц истинности (см. правило 15).
