Лекция №6а план лекции
Этапы развития логики
ТАБЛИЦА базовых логических операций
Законы алгебры логики
1-й ЭТАП связан с работами ученого и философа Аристотеля (384-322 г.г. до н.э.). Он пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Аристотель впервые дал систематическое изложение логики. Так возникла формальная логика. 2-й ЭТАП – Основы математической логики заложил немецкий ученый и философ Г.В. Лейбниц (1646-1716).. 3-й ЭТАП- Англичанин Д. Буль (1815-1864) считается основоположником АЛГЕБРА ЛОГИКИ как самостоятельной дисциплины. Так возникла АЛГЕБРА ЛОГИКИ
РАССМОТРИМ ТРИ БАЗОВЫХ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Логическая операция |
Обозначение знаками |
Таблица истинности |
Логическая операция |
|||||||||||||||
ИНВЕРСИЯ (отрицание) NOT |
|
|
Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. |
|||||||||||||||
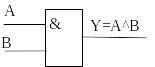
КОНЪЮНКЦИЯ (Логическое умножение) AND |
|
|
Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны. |
|||||||||||||||
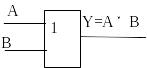
ДИЗЪЮНКЦИЯ (Логическое сложение) OR |
|
|
Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. |
|||||||||||||||
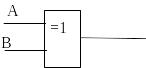
XOR (исключающий ИЛИ) |
Y=(
+(A
|
А
В
Y
1
1
0
1
0
1
0
1
1
0
0
0 |
Логическая функция ложно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны |
|||||||||||||||
NXOR
ЭКВИВАЛЕНТНОСТЬ
(Логическое равенство) |
Y=(
)
+(A
B)
|
|
Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны |
)
)
