27. Регулирование активной и реактивной мощности синхронного двигателя

Рассмотрим на примере неявнополюсного двигателя. Если пренебречь активным сопротивлением обмотки якоря, то векторную диаграмму строят по уравнению:

Регулирование активной мощности . Допустим, что двигатель работает при значении нагрузочного момента М_вн и постоянном токе возбуждения с cosφ₁=1, чему на векторной диаграмме соответствуют ток I₁₁ и угол Θ₁.

С повышением нагрузки увеличивается угол между векторами Е_f и -U_c до значения Θ₂, так как вращающий момент М_эм= М_вн пропорционален sinΘ. При этом конец вектора Е_f перемещается по окружности с радиусом Е_f. При условиях I_f = const, Е_f =const; U_c=const вектор тока I₁₂ также поворачивается вокруг точки О, располагаясь перпендикулярно вектору -jI₁₂х₁. Из диаграммы видно, что ток I₁₂ имеет отстающую реактивную составляющую.

Если нагрузка двигателя уменьшается по сравнению с исходной, то угол Θ уменьшается до значения Θ₃. При этом ток двигателя I₁₃ имеет опережающую реактивную составляющую.

Следовательно, изменение активной мощности синхронного двигателя приводит к изменению его cosφ. При уменьшении нагрузки вектор тока поворачивается в сторону опережения и двигатель может работать с cosφ=1 или с опережающим током. При увеличении нагрузки вектор тока поворачивается в сторону отставания.

Регулирование реактивной мощности. Если при неизменной активной мощности изменять ток возбуждения, то будет изменяться только реактивная мощность, т. е. величина cosφ.

Если двигатель работает при cosφ=1, то этому режиму соответствует ЭДС Е_f1, угол Θ₁ и ток I₁₁. Вектор тока перпендикулярен вектору -jI₁₁х₁.

При уменьшении тока возбуждения ЭДС снижается до Е_f2. Так как активная мощность остается неизменной:

.

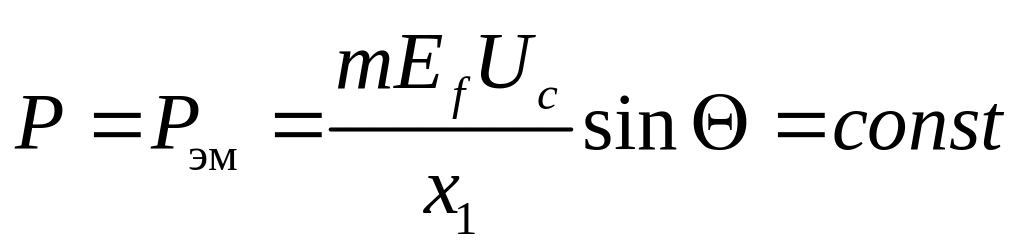то должно быть Е_f cos Θ = const. Тогда нагрузочный угол Θ увеличивается до значения Θ₂ На диаграмме это выражается в том, что конец вектора Е_f скользит по прямой CD, параллельной вектору напряжения – U_c. Вектор -jI₁₂х₁ поворачивается относительно точки А. Вектор тока I₁₂ перпендикулярен вектору -jI₁₂х₁. Следовательно вектор I₁₂ также поворачивается. При этом изменяется угол φ.

Р =m₁U_cI₁ cosφ₁= const

При работе на сеть большой мощности U_c = const, следовательно, при изменении тока возбуждения I₁cosφ₁ = const. На векторной диаграмме это выражается в том, что конец вектора I₁ скользит по прямой DE, перпендикулярной вектору напряжения U_c.

Аналогично при увеличении тока возбуждения ЭДС Е_f возрастает до Е_f3 и угол Θ₃ становится меньшим Θ₁. Вектор -jI₁₃х₁ поворачивается вокруг точки А и соответственно ему изменяет направление вектор тока I₁₃.

По диаграмме можно построить U-образные характеристики двигателя I₁=f(I_f).

28. Характеристики синхронных двигателей

U-образные характеристики I₁=f(I_f) двигателя имеют такую же форму, как и характеристики генератора.

Д

Рис. U-образные характеристики синхронного двигателя

ля двигателя угол сдвига фаз φ принято отсчитывать от вектора напряжения сети U_c. У двигателя в режиме холостого хода ток статора не равен нулю при I_f=I_fн.

При недовозбуждении ток I₁ отстает от напряжения сети U_c, т. е. двигатель потребляет из сети реактивную мощность.

При перевозбуждении ток I₁ опережает напряжение сети U_c, т. е. двигатель отдает в сеть реактивную мощность.

Это значит, что синхронный двигатель может работать в качестве двигателя и в качестве генератора реактивной мощности.

Это свойство используется для повышения cosφ электрических сетей.

Рабочие характеристики синхронного двигателя — это зависимости потребляемой мощности P₁, момента на валу M₂, тока статора I₁, коэффициента мощности cosφ₁, частоты вращения ротора n₂ и КПД η от отдаваемой механической мощности на валу двигателя P₂, т.е. P₁, M₂, I₁ , cosφ₁, n₂, η = f (P₂) при U_c = const, f_c = const, I_f = const.

Частота вращения ротора n₂=n₁ = const, так как f_c = const. Поэтому зависимость n₂=f(P₂) представляет собой прямую линию, параллельную оси ординат.

Момент на валу двигателя равен . Поэтому M₂=f(P₂) линейна при n₂= const.

Потребляемая мощность P₁, зависит от потерь. Потери в стали практически не зависят от нагрузки, а электрические потери в обмотках зависят от квадрата нагрузки. Поэтому кривая , имеет нелинейный характер.

Коэффициент мощности cosφ₁ зависит от тока возбуждения. Синхронные двигатели могут работать при cosφ₁=1, но обычно их рассчитывают на работу с перевозбуждением при номинальной нагрузке с опережающим током и cosφ₁=0,9. В этом случае двигатель отдает реактивную мощность в сеть, что улучшает суммарный cosφ сети. Создаваемая синхронным двигателем опережающая реактивная составляющая тока I₁ компенсирует отстающую реактивную составляющую тока асинхронных двигателей. При снижении нагрузки двигателя и I_f = const активная составляющая тока I₁ уменьшается, а реактивная составляющая увеличивается, угол φ₁ увеличивается, а cosφ₁ уменьшается. При увеличении нагрузки, наоборот cosφ₁ увеличивается. Зависимость cosφ₁ = f (P₂) при работе машин с перевозбуждением имеет максимум в области P₂> P_н.

Ток в обмотке статора равен I₁=Р₁/m₁U_c cosφ₁. Ток I₁ при холостом ходе является практически реактивным. По мере роста нагрузки возрастает активная составляющая тока и cosφ₁. Потребляемая мощность также растет. При этом Р₁ и cosφ₁ изменяются с разной скоростью. Зависимость I₁=f(P₂) является нелинейной.

КПД двигателя, как и потребляемая мощность, зависит от потерь. Кривая η = f (P₂) имеет характер общий для всех электрических машин.