Векторные программы

Изображение, созданное в векторных программах, основывается на математических формулах, а не на координатах пикселов. Составляющие основу таких изображений

кривые и прямые линии называются векторами. Так как при задании объектов на экране используются математические формулы, то отдельные элементы, изображения, создаваемые в векторных программах, – например, Adobe Illustrator, CorelDRAW и Macromedia FreeHand, – можно легко перемещать, увеличивать или уменьшать без проявления «эффекта ступенек». Так, для перемещения объекта достаточно перетащить его мышью. Компьютер автоматически пересчитывает его размер и новое местоположение.

Поскольку в этом случае изображение создаѐтся математически, векторные

программы используются тогда, когда нужны чѐткие линии. Они часто применяются при создании логотипов, шрифтов для вывода на плоттер и различных чертежей.

Когда вы видите изображение, созданное в векторной программе, его качество зависит не от исходного разрешения изображения, а от разрешающей способности

устройства вывода (монитора, принтера, плоттера…). Так как качество изображения не основывается на разрешении, то изображение, созданное в векторных программах, как

правило, имеет меньший объѐм файлов, чем построенное в программах побитового отображения. В векторных программах нет проблем и со шрифтами – большие

шрифтовые массивы не образуют файлов огромного размера.

Фрактальные программы

Фрактал - это объект довольно сложной формы, которая получена в результате

выполнения простого итерационного цикла над формой начальной, элементарной.

Одним из основных свойств фракталов является самоподобие. Объект называют

самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга.

Таким образом, в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале. Например, снежинка несет информацию о снежном сугробе, а горный камень имеет те же самые очертания, и что и горный хребет. Благодаря этому свойству можно использовать фракталы для генерирования поверхности местности, которая походит на саму себя, независимо от масштаба, в котором она отображена. Программы, получающие в последнее время широкое распространение и созданные по принципу генерации самоподобных фигур, явлются прекрасным инструментом в руках дизайнера, художника, разработчика WEB-приложений.

Отдельное перспективно напрвление развития фрактальных программ — создание

алгоритма фрактального сжатия графической информации.

Более подробно о фрактальной графике будет рассказано в главе 5.

Глава 2. Координаты и преобразования

2.1 Координатный метод

Координатный метод был введен в XVII веке французскими математиками Р. Декартом и П. Ферма. На этом методе основывается аналитическая геометрия, которую

можно считать фундаментом КГ. В современной КГ координатный метод широко используется.

2.1.1. Преобразование координат

Сначала рассмотрим общие вопросы преобразования координат. Пусть задана п- мерная система координат в базисе (k₁, k₂,.... k_n), которая описывает положение точки в пространстве с помощью числовых значений к_i. В КГ наиболее часто используются двумерная (n = 2) и трехмерная (n = 3) системы координат.

Если задать другую, N-мерную, систему координат в базисе (m₁, m₂,..., т) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

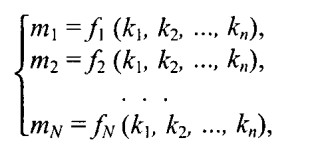
где f_i — функция пересчета i-й координаты, аргументами являются координаты в системе k_i,. Можно поставить и обратную задачу: по известным координатам (m₁, m₂,.... т) определить координаты (к₁, k₂,..., к_n ). Решение обратной задачи запишем так:

где F_i — функции обратного преобразования.

В случае если размерности систем координат не совпадают (п ≠ N), осуществить

однозначное преобразование координат чаще всего не удается. Например, по двумерным

экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.

Линейные преобразования наглядно записываются в матричной форме:

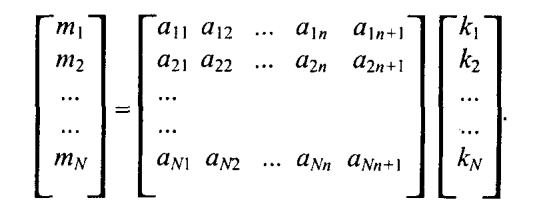
Здесь матрица коэффициентов (а_ij) умножается на матрицу-столбец (k_i), и в результате будем иметь матрицу-столбец (m_i ).

Мы и дальше часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц —

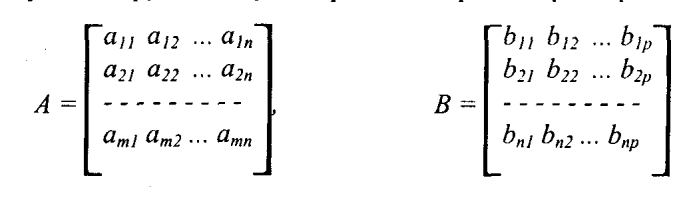
матрицы А размерами (т х п) и В — (n x p):

матричным произведением является матрица С = АВ размерами (m х р):

С = 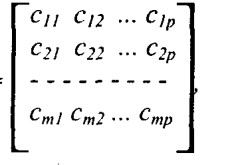для которой элементы c_ij рассчитываются по формуле

Простейшие двумерные преобразования

Точки на xy-плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки Р(х, у), которая

перемещается в новую точку Р'(х, у), сдвигаясь на Dx единиц параллельно оси x и на Dy

единиц параллельно оси у, можно написать уравнения:

На рис. 2.1 показана точка с координатами (1, 2), которая смещается на расстояние (5, 7), преобразуясь в точку (6, 9). Определяя векторы-строки

можно переписать это уравнение в векторной форме или более кратко

Объект можно перенести, применяя вышевыведенное уравнения к каждой его точке. Однако, поскольку каждый отрезок, описывающий объект, состоит из бесконечного числа точек, такой процесс длился бы бесконечно долго. К счастью, все точки, принадлежащие отрезку, можно перенести путем перемещения одних лишь крайних точек отрезка и последующего вычерчивания нового отрезка между получившимися в результате точками. Это справедливо также для масштабирования (растяжения) и поворота. На рис.

1. показан результат действия на контур домика операции переноса на расстояние (3, -4).

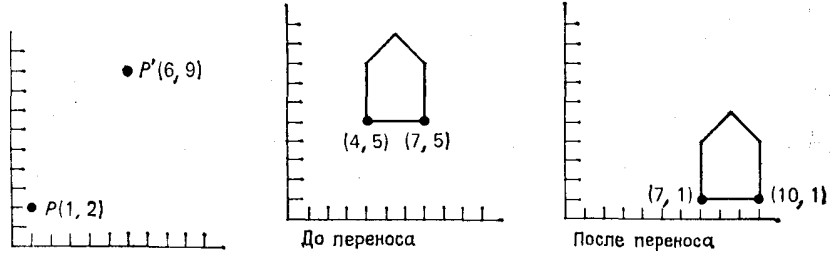
Рис. 2.1 Простейший перенос

Точки можно промасштабировать (растянуть) в Sx раз вдоль оси x: и в Sy раз вдоль оси у, получив в результате новые точки, с помощью умножения

Определяя S как , можно записать в матричной форме

или

На рис. 2.2 отдельная точка (6, 6) масштабируется с коэффициентами 1/2 по оси X и 1/3 по оси у. На этом же рисунке показан контур домика, промасштабированный с коэффициентами 1/2 по оси x и 1/4 по оси у. Отметим, что масштабирование производится относительно начала координат; в результате преобразования домик стал меньше и ближе к началу координат. Если бы масштабные множители были больше 1, то домик увеличился бы и отдалился от начала координат. Способы проведения масштабирования относительно других точек, отличных от начала координат, рассматриваются в одном из последующих разделов главы. Пропорции домика также изменились· было применено

неоднородное масштабирование, при котором Sх≠ Sу. Однородное масштабирование, для

которого Sx=Sy, не влияет на пропорции.

Точки могут быть повернуты на угол θ относительно начала координат, как показано на рис. 2.2 для точки Ρ (6, 1) и угла θ = 30°. Математически поворот определяется следующим образом:

В матричной форме мы имеем

или

где через R обозначена матрица поворота. На рис. 2.2 показан квадрат, повернутый на 45°. Как и в случае масштабирования, поворот производится относительно начала координат.

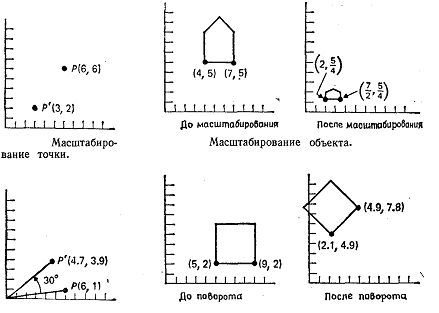
Рис. 2.2 Простейшие поворот и масштабирование