2. Вычисление нормалей и углов отражения

Вычисление координат вектора нормали. Рассматривая модели отражения света, вы, наверное, обратили внимание на то, что нормаль к поверхности — важный элемент.

Определение вектора нормали к поверхности в заданной точке может быть выполнено разными способами. В значительной степени это определяется типом модели описания

поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных

производных функций описания. Например, если поверхность задана параметрическими функциями

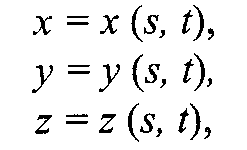
тогда координаты вектора нормали можно вычислить так:

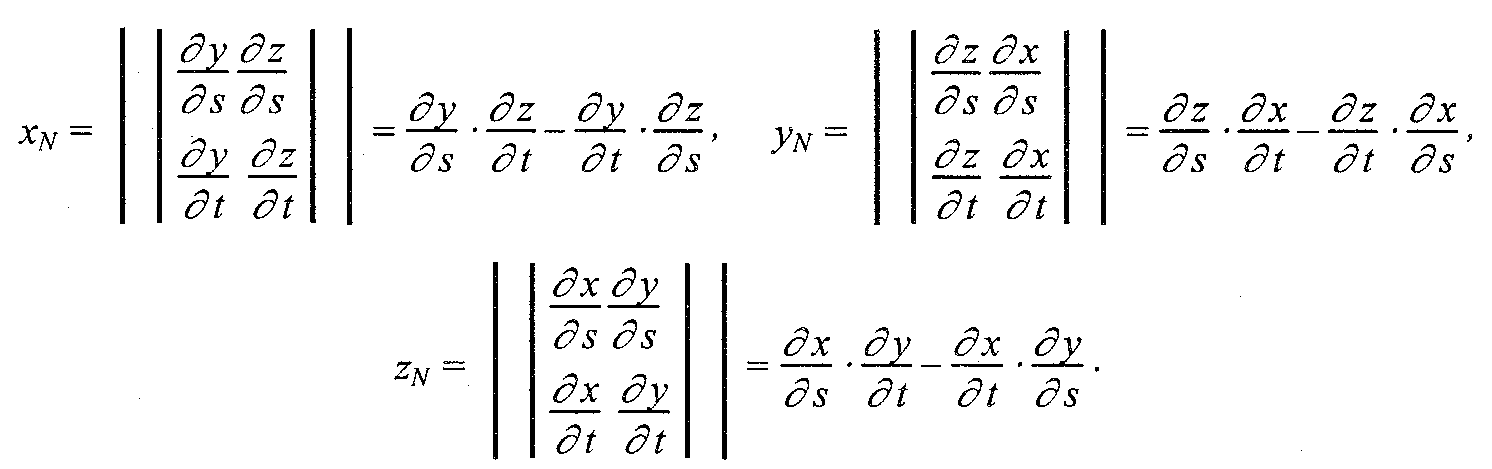
В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная поверхность. Рассмотрим

одну ее плоскую грань, имеющую вид треугольника (рис. 8.4).

Для вычисления координат вектора нормали воспользуемся векторным

произведением любых двух векторов, которые лежат в плоскости грани. Такими векторами могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены нами только для радиус-векторов. Чтобы перейти к радиус-векторам, введем новую систему координат, центр которой совпадает с вершиной 1, а оси — параллельны осям бывшей системы. Координаты вершин в новой системе:

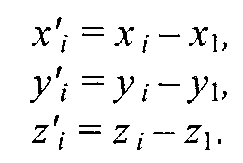
Рис. 8.4. Одна грань поверхности Радиус-векторы

Теперь назовем ребро (1-2) вектором А, а ребро (1-3) — вектором В, как показано на рис.

4. Таким образом, положение нормали к грани в пространстве будет описываться радиус-

вектором N. Его координаты в системе (х', у', г') выразим формулами для векторного произведения

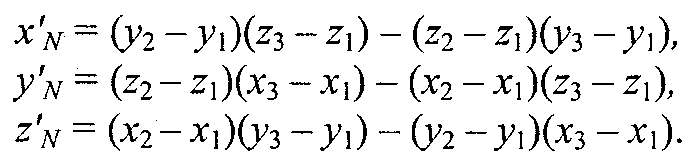
Плоская грань может быть изображена в разных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, которое соответствует видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать для нормали обратный вектор, то есть (- N).

Если полигональная поверхность имеет не треугольные грани, а, например, плоские четырехугольные, то расчет нормали можно выполнять по любым трем вершинам грани.

Диффузное отражение. Рассчитаем косинус угла между вектором нормали и направлением на источник света. Это можно выполнить таким способом.

Сначала необходимо определить радиус-вектор, направленный на источник света.

Обозначим его как S. Потом для вычисления косинуса угла между радиус-векторами S и N воспользуемся формулами скалярного произведения векторов. Поскольку

а также

то получим

Для упрощения вычислений целесообразно использовать векторы S и N единичной длины, то есть |S|*|N| = 1.

Использование скалярного произведения здесь можно считать универсальным методом, который можно использовать для любого расположения точечного источника

света. В отдельных случаях можно рассчитать косинус угла падения по-иному. Например, если источник света располагается на оси Z видовых координат в бесконечности позади

камеры, тогда косинус угла нормали к грани с осью Z равняется отношению координаты г и длины радиус-вектора нормали

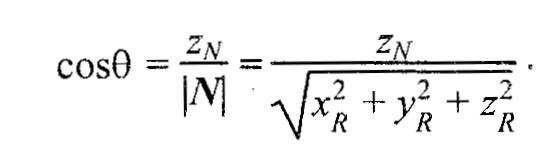
Зеркальное отражение. Будем считать, что задан радиус-вектор S, направленный на источник света, а также известен радиус-вектор нормали N. Нужно найти косинус угла между отраженным лучом и направлением камеры.

Сначала необходимо вычислить радиус-вектор отраженного луча. Обозначим его как R. Выполним некоторые геометрические построения, как показано на рис. 8.5.

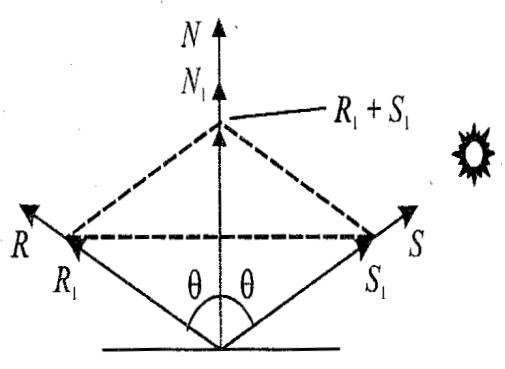
Рис. 8.5. Векторы R1, S1 и N1 –единичной длины

Для решения нашей задачи сначала рассмотрим единичные векторы R1, S1, и N1. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно записать R1 + S1 = N¹, где N¹ — это вектор, который соответствует диагонали ромба и совпадает по yаправлению с нормалью. Длина вектора N1 равняется 2cos . Поскольку вектор N¹ по направлению совпадает с N1, то

или

Отсюда находится единичный вектор отраженного луча:

Найдем cos . Для этого используем скалярное произведение векторов N и S:

Подставим это значение в выражение для R₁:

Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, т.е. R = S R₁ , получим:

Это решение в векторной форме. Запишем координаты вектора R:

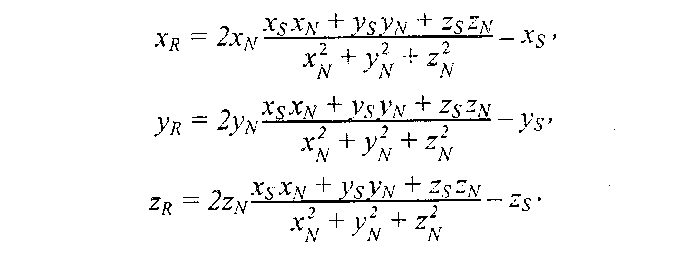
Теперь осталось найти косинус угла между отраженным лучом и направлением камеры. Пусть K – радиус-вектор, направленный на камеру. Найдем искомый косинус угла:

Для упрощения вычислений целесообразно задавать векторы S, N и R единичной длины (тогда и R будет единичным).