Глава 7. Методы и алгоритмы построения сложных трехмерных объектов

Понятие ―трехмерная‖ графика в настоящее время можно считать наиболее распространенным для обозначения темы, которая будет рассмотрена ниже (в литературе это название часто сокращается до "ЗD-графики"). Однако необходимо заметить, что такое название неточное, так как речь пойдет о создании изображения на плоскости, а не в объеме. Действительно трехмерные средства отображения пока что недостаточно широко распространены.

1. Модели описания поверхностей

Для описания формы поверхностей могут использоваться разнообразные методы. Сделаем обзор этих методов.

1. Аналитическая модель

Аналитической моделью будем называть описание поверхности математическими формулами. В КГ можно использовать много разновидностей такого описания. Например,

в виде функции двух аргументов z = f(x, у). Можно использовать уравнение F(x, у, z) = 0.

Наиболее часто используется параметрическая форма описания поверхности.

Запишем формулы для трехмерной декартовой системы координат (x, у, z):

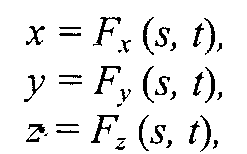
где s и t — параметры, которые изменяются в определенном диапазоне, а функции

F_x, F_y,и F_z определяют форму поверхности.

Преимущества параметрического описания — легко описывать поверхности,

которые соответствуют неоднозначным функциям, замкнутые поверхности. Описание можно сделать таким образом, что формула не будет существенно изменяться при поворотах поверхности, масштабировании.

В качестве примера рассмотрим аналитическое описание поверхности шара.

Сначала как функцию двух аргументов:

z = ±

_R2 _x2 _y 2

В виде уравнения: x² + y² + z² - R²=0.

А также в параметрической форме:

x = R sins cost, y = R sins sint, z = R coss.

Для описания сложных поверхностей часто используют сплайны. Сплайн - это

специальная функция, наиболее пригодная для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образуют модель сложной поверхности. Другими словами, сплайн — эта тоже поверхность, но такая, для которой можно достаточно просто вычислить координаты ее точек. Обычно используют кубические сплайны. Почему именно кубические? Так как третья степень является наименьшей, позволяющей описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную — такая поверхность будет без излома в местах стыка. Сплайны часто определяют параметрически. Запишем формулу для координаты x(s,t ) кубического сплайна в виде многочлена третьей степени параметров s и t:

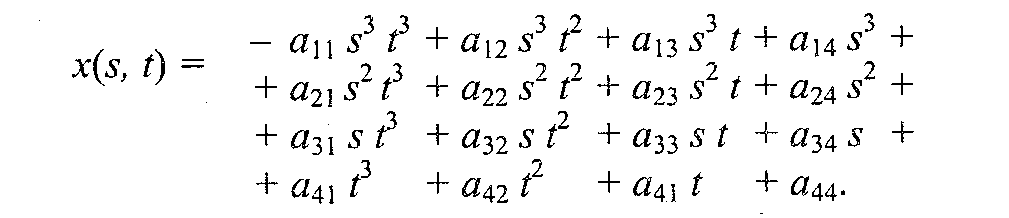
Для других координат можно записать подобные формулы — в виде функций y(s, t), z(s,t).

В математической литературе вы можете ознакомиться со способами определения

коэффициентов a_ij для сплайнов, которые имеют заданные свойства.

Рассмотрим одну из разновидностей сплайнов — сплайн Безье. Приведем его

сначала в обобщенной форме — степени т х п :

m n

i i m i j j n j

P(s,t) =

i 0

C_m s (1

j 0

s) C_n t (1

s) P_ij

m

C

и

n

^{где Р} _{i j} ^{— опорные точки-ориентиры, 0≤s ≤1 , 0≤ t ≤ 1 ,} С ^{i j –}

коэффициенты бинома Ньютона, они рассчитываются по формуле:

_{C b} a!

^a b!(a

b)!

C

и

n

Кубический сплайн Безье соответствует т = 3, п = 3. Для его определения

С

m

необходимы 16 точек-ориентиров Р _{i j} (рис. 7.1); коэффициенты ⁱ

3, 1 при i , j = 0,1,2,3.

^j равняются 1,3,

Характеризуя аналитическую модель в целом, можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхностей. С позиций КГ можно указать такие положительные черты: простота (впрочем, не всегда) расчета координат каждой точки поверхности, нормали; небольшой объем информации для описания довольно сложных форм.

К недостаткам можно отнести: сложность формул описания с использованием функций, которые медленно вычисляются в компьютере, снижают скорость выполнения операций отображения; невозможность в большинстве случаев использования данной формы описания непосредственно для построения изображения поверхности. В таких случаях поверхность обычно отображают как многогранник, используя формулы аналитического описания для расчета координат вершин граней в процессе отображения, что уменьшает скорость сравнительно с полигональной моделью описания.

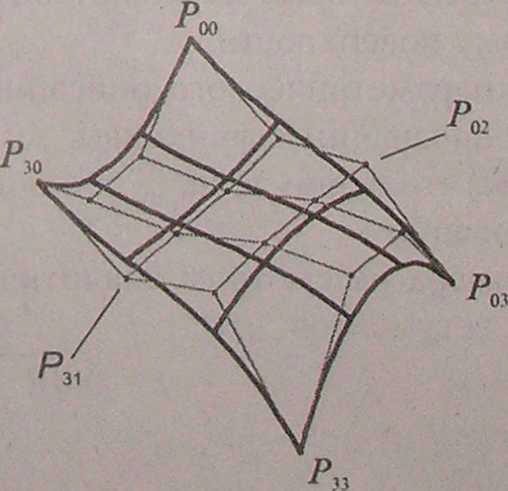
Рис. 7.1. Кубические сплайны Безье