3.3Внутренняя энергия системы

Полная энергия т. системы равна сумме кинетической энергии механического движения системы как целого, потенциальной энергии системы во внешнем поле ( гравитационном или электромагнитном) и внутренней энергии , зависящей только от внутреннего состояния системы. Для неподвижных систем, не подверженных действию внешних сил, значение полной и внутренней энергий совпадают.

Внутренняя энергия включает в себя энергии всевозможных видов движения и взаимодействия всех частиц (молекул, атомов, ионов и др.) системы, Например, для газа внутренняя энергия состоит из:

а) кинетической энергии теплового поступательного и вращательного движения молекул, а также колебательного движения атомов в молекулах;

б) потенциальной энергии, обусловленной силами межолекулярного взаимодействия;

в) энергии электронных оболочек атомов и ионов;

г) энергии движения и взаимодействия нуклонов в ядрах.

Внутренняя энергия является однозначной функцией состояния т.системы, Ее значение в каком –либо произвольном состоянии системы не зависит от того, каким образом пришла система в это состояние. Т.е., изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса перехода и равно . В частности, если система возвращается в результате какого-либо перехода в исходное состояние, то полное изменение внутренней энергии равно нулю.

Подобно потенциальной энергии в механике, определяется с точностью до постоянной величины , зависящей от выбора отсчета внутренней энергии, т.е., от выбора нуля. Так, как во всех расчетах термодинамики находят не абсолютное значение внутренней энергии, а ее изменение , то выбор не играет роли.

Составляющие внутренней энергии в) и г) не изменяются во всех процессах, не связанных с химическими реакциями и другими превращениями электронных оболочек атомов и ионов, а также ядерными реакциями и их можно не включать во внутреннюю энергию. Поэтому в дальнейшем под внутренней энергией в термодинамике будем понимать только сумму кинетической энергии теплового механического движения молекул и потенциальной энергии их взаимодействия. В идеальном газе последнее слагаемое равно нулю, значит его внутренняя энергия равна сумме кинетических энергий беспорядочного движения всех молекул.

3.3Работа и теплота

Обмен энергией между т.системой и внешними телами может происходить двумя качественно различными способами: путем совершения работы и путем теплопередачи. Первый способ, как известно из механики, осуществляется при силовом взаимодействии между телами. Энергия, передаваемая при этом т. системе внешними телами, называется работой, совершаемой над системой

Энергия, передаваемая внешними телами путем теплообмена, называется теплотой, получаемой т. системой от внешней среды.

Для совершения работы над неподвижной системой необходимо, чтобы перемещались внешние тела, т.е., чтобы изменялись внешние параметры состояния системы.

В отсутствии внешних силовых полей обмен энергией между неподвижной системой и внешней средой путем совершения работы происходит только при изменении объема и формы системы. Например, работу над газом производят силы давления на газ со стороны внешней среды. При этом работа внешних сил над системой , численно равна и противоположна по знаку работе , совершаемой самой системой над внешней средой, т.е., против внешних сил.

В отличие от внутренней энергии системы, являющейся однозначной функцией состояния этой системы, понятие теплоты и работы имеют смысл только в связи с видом процесса изменения состояния системы. Они являются энергетическими характеристиками конкретного процесса.

Существует качественное различие между совершением работы и теплообменом, как способами обмена энергией между макросистемами. Совершение работы над системой может изменить любой вид энергии системы. Например, при неупругом соударении тел часть совершенной работы идет на изменение кинетической энергии, а часть работы – на приращение внутренней энергии. Если же энергия сообщается в виде теплоты, то она идет только на увеличение энергии теплового движения молекул, т.е. на .

Б-2

1. Вектор перемещения, элементарное перемещение и путь, средняя и мгновенная скорость.

Вектором перемещения точки за промежуток от до называется приращение радиус-вектора этой точки за этот промежуток он направлен вдоль хорды стягивающий соответствующий участок траектории точки. Поэтому во всех случаях, кроме премера, модуль перемещения меньше длины пути за этот же . На рисунке вектор перемещения .

Однако, по мере уменьшения длины пути разность между хордой и перемещением уменьшается. Следовательно, рассматривая элементарное перемещение по траектории за достаточно малый промежуток вреени (от до ) можно пренебречь отличием между и . Значит, вектор направлени по касательной к траектории в сторону движения точки. Также ка единичный вектор касат. т.о. вектор перемещения материальной точки за любой конечный промежуток времени от до можно представить в виде:

приращение координат за .

P.S.: В математике и - дифференциалы соответствующих функций времени ??? т.е. линейные части приращений этих функций при произвольном изменении аргумента от до . По определению в мтематике ,

а ;

и - производные т.е. приращение функций и существует отличие от дифференциалов этих функций. В физике различают произвольное (конечное) приращение аргумента и дифференциала аргумента . Под дифференциалом аргумента понимают столь малое его приращение (элементарное), при котором разностью между соответствующим приращением функции и линейной частью её приращения можно пренебречь т.е. ??? . Поэтому, в физике используют предложенные Лейбницем обозначение производной и трактуют эти выражения как отношения не математической дифференциала функции и аргумента, а малых (элеиентарных) приращений функцмм м аргумента.

Скорость.

Д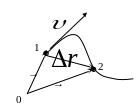 ля характеристики направления и быстроты движения точки вводится векторная физическая величина-скорость.

Пусть за точка переместилась из т.1 в т.2. Вектор перемещения представляет собой приращение радиус-вектора за время . Отношение называется средней скоросью точки за время . Направление совпадает с . Скорость точки в заданный момент мремени определяется как предел отношения при т.е.

т.е. производной от радиус-вектора по времени и направлению по касательной к траектории в заданной точке в сторону движения. Модуль . Вектор можно разложить по базису т.е. на три состояния по осям декартовой системы координат

;

; ; ;

;

2. Уравнение динамики вращения твердого тела.

Уравнение динамики твердого тела можно получить. Записав для производной момента импульса

(уравнение моментов)

и подставив значение для твердого тела, вращающегося вокруг произвольной оси ;

;

(*) ;

—суммарный момент всех внешних сил относительно оси вращения . Отсюда видно, что (сравнивая с II-ым законом Ньютона) во вращательном движении тела роль массы играет , а роль линейного ускорения играет угловое ускорение , а роль результирующей силы —суммарный момент внешних сил . определяет инерциальные свойства. Если масса не зависит от выбора С.О. то зависит от оси. Относительно которой определяется.

Интегрирование уравнения (*) с учетом начальных условий и при позволяет полностью решить задачу о вращении твердого тела, т.е. найти , в любой момент времени в системе отсчета, жестко связанной с осью вращения.

3. Температура. Шкала Цельсия, термодинамическая температурная шкала.

Температура системы, находящейся в равновесном состоянии, является мерой интенсивности теплового движения молекул, образующих систему. В этом состоит молекулярно-кинетическое истолкование температуры.

Если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е., не обмениваются энергией путем теплопередачи, то им приписывают одинаковую температуру, а если при тепловом контакте одно из них передает энергию другому посредством теплопередачи, то первому приписывают большую температуру, второму – меньшую.

Средняя кинетическая энергия теплового движения частиц прямо- пропорциональна термодинамической температуре системы.

Для измерения температуры используется зависимость от температуры ряда физических свойств тела, называемого термометрическим, при прямом или косвенном измерении: длина, объем, сопротивление и др. Их изменение является основой для измерения температуры.

Для практического измерения температуры применяются температурные шкалы, установленные с помощью термометрических тел. В Международной стоградусной шкале в качестве термометрического тела берется вода и температура выражается в градусах Цельсия. В термодинамической температурной шкале температура выражается в К и называется термодинамической температурой. Связь между шкалами . К называется абсолютный нуль температуры или нуль по термодинамической

Б-3

1. Ускорение, тангенциальное и нормальное ускорение.

Движение точки характеризуется также ускорением—быстротой изменения скорости

;

т.е. вектор равен производной по времени. Направление вектора совпадает с направлением приращения скорости за т.к. , то ускорение точки равно второй производной по времени от радиус-вектора:

;   ;   ;

где —проекция.

Если траектории точки плоская кривая, то можно выбрать два перпендикулярных направления: касательная к траектории (орт ) и нормали к ней . Тогда раскладывается по составляющим .

Т.к. вектор скорости направлен по касательной к траектории в сторону её движения, то

;

;

;

тогда ; —приращение орта касательной к траектории, соответствующее элементарному пути за .

В виду малости его можно считать совпадающим с дугой окружности радиуса с центром в т.0 с центральным углом .

С

0

оответственно, единичный вектор повор. на . Из равнобедренного треугольника , ввиду малости ; по направлению совпадает с (при )

;

и ускорение точки

;

— касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении и совпадает с , при замедленном и не совпадает с . Нормальное ускорение характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории; ; поэтому его называют центростремительным. При прямолинейном движении .

М одуль ускорения

;

При ускоренном движении — острый, при замедленном—тупой ( угол между и ). Если движение по окружности равномерное то касательной.

2. Принцип работы гироскопа.

При воздействии по оси чувствительности момента внешней силы, стремящейся изменить направленность в пространстве оси собственного вращения, эта ось гироскопа начинает отклоняться не по оси действия момента, а по перпендикулярной ей. В результате гироскоп вращается вокруг измерительной оси, перпендикулярной направлению вектора приложенного момента (явление прецессии).

Данное свойство напрямую связано с возникновением так называемой кориолисовой силы. Так, при воздействии момента внешней силы гироскоп поначалу будет вращаться именно в направлении действия внешнего момента (нутационный бросок). Каждая частица гироскопа будет таким образом двигаться с переносной угловой скоростью вращения из-за момента. Но роторный гироскоп, помимо этого, и сам вращается, значит, каждая частица будет иметь относительную скорость. Следовательно, возникнет кориолисова сила, которая будет заставлять гироскоп двигаться в перпендикулярном приложенному моменту направлению, то есть прецессировать. Прецессия вызовет кориолисову силу, момент которой скомпенсирует момент внешней силы.

Гироскопический эффект вращающихся тел есть проявление коренного свойства материи — её инертности.

Упрощённо, поведение гироскопа описывается уравнением:

,

где векторы и являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр  — его моментом инерции, векторы и угловой скоростью и угловым ускорением.

Отсюда следует, что момент силы , приложенный перпендикулярно оси вращения гироскопа, то есть перпендикулярный , приводит к движению, перпендикулярному как , так и , то есть к явлению прецессии. Угловая скорость прецессии гироскопа определяется его моментом импульса и моментом приложенной силы:

,

то есть обратно пропорциональна скорости вращения гироскопа.