4 Пошаговая реализация метода экспертных оценок и ранговой корреляции к задаче выбора лучшего педагогического отряда города Оренбурга

Ниже приведена пошаговая реализация метода экспертных оценок к задаче выбора лучшего педагогического отряда.

Шаг 1. Областным штабом был составлен список факторов , оказывающих влияние на выбор лучшего СПО. Затем экспертам, в роли которых выступали лучшие социальные работники города, были предложены анкеты. Заполняя анкету, эксперт определял место факторов в ранжированном ряду. Вклад каждого фактора оценивался по величине ранга-места (а_ij), которое отводилось экспертом данному фактору при ранжировании всех факторов с учетом их предполагаемого влияния. Фактору, которому приписывалась ведущая роль, отводилось первое место (ранг 10), остальные располагались в порядке убывания степени их влияния на выбор лучшего педагогического отряда. Если было трудно определить превалирующее влияние какого-то фактора над другим, то им присваивались одинаковые ранги.

В результате таких действий получается ранжирование факторов по степени важности. Результаты работы m экспертов относительно k факторов сводятся в матрицу размера (m × k), которая называется матрицей опроса. Вид матрицы приведен на рисунке 3.4.

Факторы	Эксперты
	1	2	…	j	…	M
1 2 … i … K	a11 a21 … ai1 … a1m	a12 a21 … ai2 … a2m	… … … … … …	a1j a2j … aij … amj	… … … … … …	a1m a2m … aim … akm

Рисунок 3.4 – Матрица опроса

Шаг 2. Данные опроса обрабатываются следующим образом. Для каждого фактора находят сумму рангов 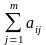_, где m – число опрошенных клиентов, а_ij - ранг i-го фактора, присвоенный j-м экспертом. Затем вычисляют отклонение ∆ суммы рангов от средней суммы рангов для каждого из факторов:

(3.8)

где ∆_i – отклонение суммы рангов i-го фактора от средней суммы рангов;

k – число факторов;

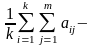средняя сумма рангов.

Иногда возникает ситуация, при которой эксперт, присваивая факторам ранги по степени их влияния, не может разграничить два или большее число членов ряда. В этом случае использует так называемые «связанные» ранги. В этом случае в матрицу опроса добавляется столбец с величиной T_j, которая находится следующим образом:

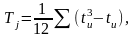(3.9)

где u – число групп, образованных факторами одинакового ранга, в j-ом ранжировании;

t_u – число одинаковых рангов в u-ой группе j-го ранжирования.

Вид обработанной матрицы опроса представлен на рисунке 3.5, где ∆²_i – квадрат отклонений, необходимый для расчета коэффициента конкордации.

Эксперты	Ранги по факторам							Tj
	1	2	…	j	…	k
1 2 … i … M	a11 a21 … ai1 … a1m	a12 a21 … ai2 … a2m	… … … … … …	a1j a2j … aij … amj	… … … … … …	a1k a2k … aik … amk
Сумма рангов			…		…
Отклонение ∆i	∆1	∆2	…	∆j	…	∆k
Квадрат отклонения ∆2i	∆21	∆22	…	∆2j	…	∆2k

Рисунок 3.5 – Обработанная матрица опроса

Шаг 3. Одним из недостатков метода экспертных оценок является субъективность экспертных оценок, поэтому для повышения степени объективности оценки проводится ранжирование сразу несколькими экспертами-клиентами.

Необходимо оценить степень согласованности мнений опрошенных экспертов. Для этого используют коэффициент конкордации (согласованности) W,

который вычисляют по формуле (3.6):

,

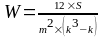где .

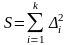Установлено, что величина m×(k - 1)×W подчиняется χ²-распределению с числом степеней свободы f = k - 1.

Значимость коэффициента конкордации W устанавливают с помощью критерия Пирсона. Для этого находят расчетное значение χ²_p:

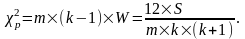(3.10)

Расчетное значение χ²_p сравнивают с табличным значением χ²_t из распределения Пирсона, найденным для принятого уровня значимости α и числа степеней свободы f = k - 1. Гипотеза о наличии согласованности мнений опрошенных экспертов принимается, если χ²_p ≥ χ²_t.

Если имеются «связанные» ранги, то коэффициент конкордации вычисляется по следующей формуле:

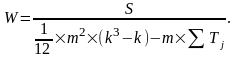(3.11)

При наличии «связанных» рангов величина χ²_p определяется по формуле:

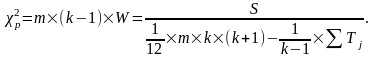(3.12)

Шаг 4. Убедившись в согласованности мнений экспертов, необходимо построить диаграмму рангов для выявления факторов, оказывающих наименьшее и наибольшее влияние на выбор лучшего педагогического отряда. При построении диаграммы по оси абсцисс откладываются факторы в порядке убывания суммы рангов, а по оси ординат суммы рангов. Степень влияния факторов на выбор лучшего педагогического отряда оценивается по величине суммы рангов: чем меньше сумма рангов фактора, тем меньшее влияние фактор оказывает на исследуемую величину и наоборот.