Новосибирский национальный исследовательскийгосударственный университет

А.И. Чанышев

О.Е. Белоусова

Тензоры напряжений и деформаций.

Тензорный базис.

Векторные представления

Методические указания

Для самостоятельной работы студентов

Новосибирск

2011

УДК: 539.374

Ч67

Ч67 Чанышев А.И. Тензоры напряжений и деформаций. Тензорный базис/ Векторные представления / А.И. Чанышев, О.Е. Белоусова // Методические указания для самостоятельной работы студентов. – Новосибирск, 17 с.

Методические указания предназначены для самостоятельной работы студентов, изучающих геомеханику, механику деформируемого твердого тела, теоретическую механику, сопротивление материалов.

Работа подготовлена на кафедре Геомеханики ГГФ НГУ

Рецензенты: д-р геол.-минерал. наук, проф. В.Д. Суворов

д-р физ.-мат. наук, проф. В.М. Жигалкин

Содержание

ПРЕДИСЛОВИЕ…….……………………………………………….…....4

1. ОПРЕДЕЛЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

ТЕНЗОРОВ 2-ГО РАНГА……………….……………………………....5

2. Примеры тензорных базисов……….....………………………6

3. ЗАКОН ГУКА ДЛЯ ПЕРВОНАЧАЛЬНО ИЗОТРОПНЫХ СРЕД

КАК ЛИНЕЙНОЕ СИММЕТРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ

ТЕНЗОРА НАПРЯЖЕНИЙ В ТЕНЗОР ДЕФОРМАЦИЙ И

нАОБОРОТ….…………………………………………………………...9

УПРАЖНЕНИЯ…..………………………………………………………15

ЛИТЕРАТУРа…..…………………………………………………..........16

Предисловие

В механике деформируемого твердого тела вообще, и в механике горных пород в частности, сложилось парадоксальная ситуация, когда для описания тензоров напряжений и деформаций со времен Л.И. Седова (1962 г.) используется понятие тензорного базиса и в то же время применяемые базисы не являются ни ортогональными, ни ортонормированными. То, что возможно определить понятие ортонормированного и ортогонального базиса указал в еще 1963 году В.В. Новожилов. Различные ортогональные и ортонормированные базисы рассматривал К.Ф. Черных (1976 г.). В эти годы (19591984) активно вводились в рассмотрение собственные тензорные базисы, связанные с исследованием закона Гука. Впервые предложил применять собственные тензорные базисы упругости для описания свойств пластичности А.И. Чанышев (1984 г.).

Данное методическое пособие призвано показать студентам преимущества определения скалярного произведения тензоров для построения тензорных ортогональных и ортонормированных базисов.

1. Определение скалярного произведения тензоров 2-го ранга

В данной точке сплошной среды напряженное и деформированное состояние характеризуются симметричными тензорами напряжений и деформаций

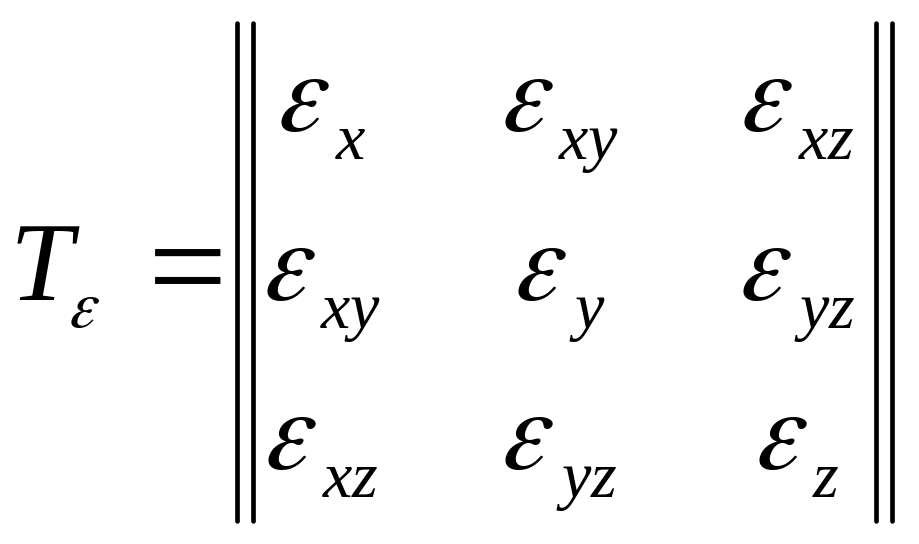, , (1)

где , ,  нормальные, а , ,  касательные напряжения на площадках, перпендикулярных к координатным осям , , ; , ,  нормальные, , ,  касательные (сдвиговые) деформации на площадках, перпендикулярных к , , .

Каждый из тензоров , определяется шестью независимыми компонентами.

Будем рассматривать эти тензоры как векторы в некотором евклидовом пространстве. Для этого необходимо ввести понятие базиса  ортогонального и ортонормированного. Для симметрических матриц порядка 33 наиболее подходящим определением скалярного произведения является след произведения двух матриц. Другими словами, если у вас есть матрица , матрица , определяемые (1), то след произведения этих матриц есть выражение

. (2)

Отметим, что (2) возможно записать в виде , где по повторяющимся индексам производится суммирование. Таким образом, скалярное произведение тензоров , (будем обозначать его как ) есть выражение

. (3)

Отметим, что скалярное произведение позволяет вводить такие понятия как длина тензора, угол между тензорами, как это принято в геометрии. Так, например, длина тензора (будем обозначать ее как ) есть величина

.

Угол между тензорами , определяется через значение , где

. (4)

Задание. Показать, что (3) действительно удовлетворяет всем аксиомам, предъявляемым к определению скалярного произведения.