Новосибирский национальный исследовательский

государственный университет

А.И. Чанышев, И.М. Абдулин

Феноменологические механические блочные модели геОсред

методические указания

для самостоятельной работы студентов

Новосибирск

2011

УДК: 539.374

Ч67

Ч67 Чанышев А.И. Феноменологические механические блочные модели геосред / А.И. Чанышев, И.М. Абдулин // Методические указания для самостоятельной работы студентов. – Новосибирск, 22 c.

Методические указания предназначены для самостоятельной работы студентов, изучающих геомеханику, механику деформируемого твердого тела, теоретическую механику, сопротивление материалов.

Работа подготовлена на кафедре Геомеханики ГГФ НГУ

Рецензенты: д-р геол.-минерал. наук, проф. В.Д. Суворов

д-р физ.-мат. наук, проф. В.М. Жигалкин

Содержание

Предисловие………………………………………………….…...4

1. БЛОЧНАЯ ФЕНОМЕНОЛОГИЧНАЯ МЕХАНИЧЕСКАЯ МОДЕЛЬ ПЕРВОНАЧАЛЬНО ИЗОТРОПНОЙ СРЕДЫ, ПОСТРОЕННАЯ ПО ЗАКОНУ ГУКА...........……………………….5

2. Формулировка соотношений пластического и запредельного деформирования………………………..11

3. ФЕНОМЕНОЛОГИЧЕСКАЯ МЕХАНИЧЕСКАЯ БЛОЧНАЯ МОДЕЛЬ ПЕРВОНАЧАЛЬНО ОРТОТРОПНОЙ СРЕДЫ………………………………………………………………..13

ЛИТЕРАТУРа....……………………………………………….…….21

Предисловие

В механике деформируемого твердого тела вообще, и в механике горных пород в частности, возникают вопросы связанные с образованием эффекта Пуассона когда силы в данном направлении не действуют, а смещения или деформации в этом же направлении есть.

В связи с этим предлагались различные схемы деформирования твердых тел. В данном пособии предлагаются две возможные схемы или модели деформирования материалов, в которых структурными элементами являются жесткие недеформируемые блоки, а вся деформация модели складывается из простейших видов деформаций – простого удлинения и простого сдвига, которые происходят без кажущегося эффекта Пуассона. Указываются достоинства и недостатки этих представлений. В рамках построенных моделей дается объяснение образования эффекта Пуассона, показывается развитие этих моделей для построения математических моделей деформирования горных пород. Пособие может быть полезным студентам геомеханикам, аспирантам, научным сотрудникам геомеханического профиля.

1. Блочная феноменологичная механическая модель первоначально изотропной среды, построенная по закону гука

Известно, что при достаточно больших деформациях на поверхностях однородных деформируемых тел наблюдаются линии или следы некоторых поверхностей скольжения материала, которые наводят на мысль, что деформируемые твердые тела состоят из блоков и многие деформации, если не все, происходят за счет подвижек одних блоков относительно других. Возникает вопрос, который заключается в следующем: на каком этапе деформирования твердых тел образуются блочные структуры? Некоторые исследователи полагают, что блоки возникают в пластичности, т. е. при пластических деформациях. Причем связаны они с действием площадок максимального касательного напряжения. Другие исследователи полагают, что блоки – результат перехода системы дифференциальных уравнений равновесия из эллиптического состояния в гиперболическое. Другими словами, линии Чернова–Людерса, обнаруживаемые на поверхностях деформируемых тел, – это характеристики системы ДУ.

Есть еще один вопрос, который заставляет обратиться к рассмотрению механизма образования деформаций. Это – эффект Пуассона. Дело в том, что все классические представления (закон движения Ньютона, закон Гука) говорят о том – куда направлена сила, туда же направлено ускорение, куда направлена сила, туда же направлено смещение. Здесь же получается парадокс: силы нет, а смещение есть.

Для ответа на эти и другие вопросы попытаемся построить феноменологическую механическую модель материала. Будем исходить из того, что эта модель нам неизвестна, известны лишь отклики этой модели. Возьмем в качестве отклика закон Гука. Попытаемся по нему восстановить модель среды. Пусть , – тензоры напряжений и деформаций соответственно. Пусть 1, 2, 3 – главные оси этих тензоров (для первоначально изотропных сред главные оси и совпадают всегда).

В системе координат 1, 2, 3 закон Гука имеет вид:

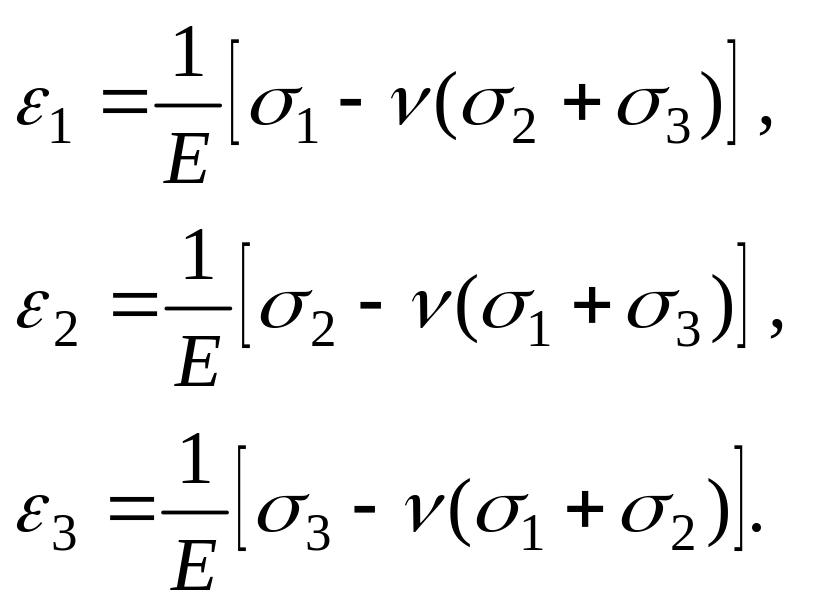(1)

где – модуль Юнга, – коэффициент Пуассона.

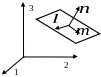
Рис. 1. Базисные орты на площадке с нормалью

В системе координат 1, 2, 3 рассмотрим произвольную площадку с нормалью ( ) и определим на ней векторы Коши , , которые представим в виде:

* ,

где символом (*) обозначается скалярное произведение тензоров и векторов; – единичные векторы касательных к данной площадке ( ). Для проекций этих векторов имеем формулы:

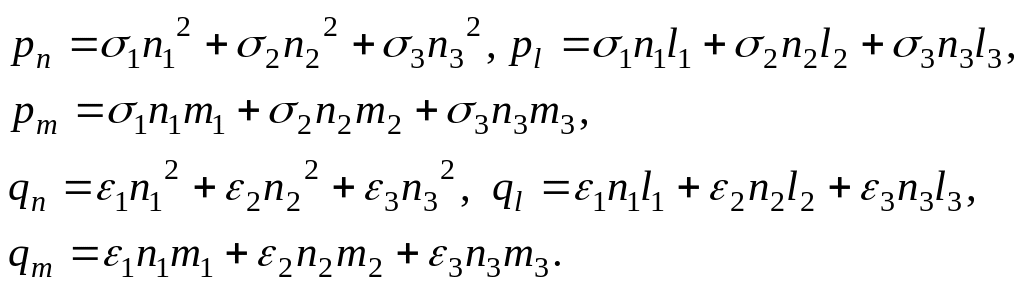(2)

Подставляя в (2) соотношения закона Гука (1), находим, что на любой площадке с нормалью

, где .

Однако значение пропорционально не везде, а только на восьми площадках, которые равнонаклонны к осям 1, 2, 3. Покажем это. Для чего вместо , , введем в рассмотрение три другие независимые величины:

. (3)

Легко проверить, что определитель преобразования здесь равен единице в силу . В самом деле имеем

.

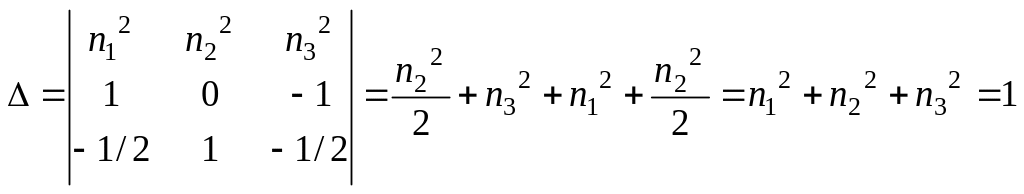Поэтому величины (как и величины , , ) – действительно независимые величины. Из (3) следует, что

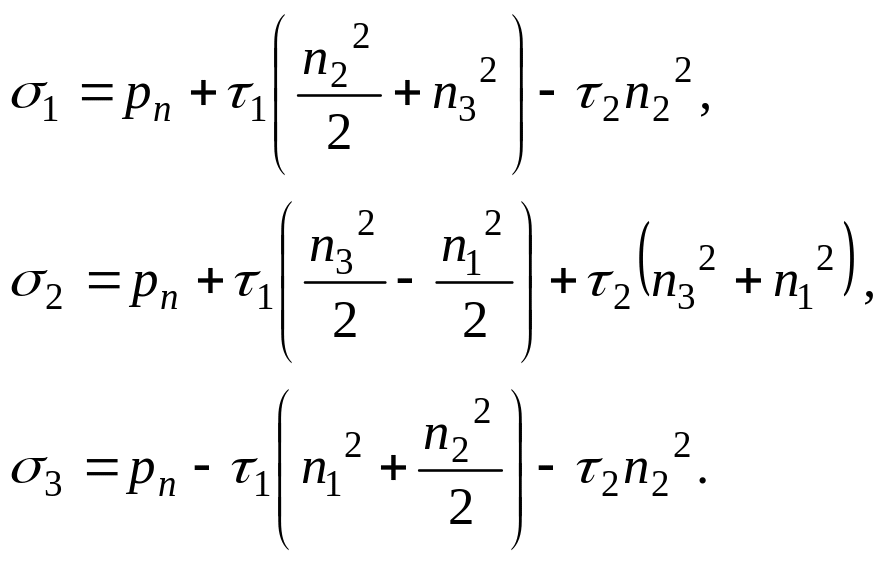(4)

Подставляя (4) в (2), в определение величины , находим

.

Полагая , где – коэффициент пропорциональности, подлежащий определению, получаем

.

В силу линейной независимости следует, что

.

Имея в виду то, что , находим

. (5)

Это и есть равнонаклонные к осям 1, 2, 3 площадки, других площадок в случае независимого изменения напряжений , , не существует, в пересечении они образуют октаэдр (рис. 2). На этих площадках таким образом имеем равенства

. (6)

Благодаря тому, что первые две формулы в (6) – это уравнения в проекциях одного векторного равенства, то (6) возможно переписать еще в виде:

(7)

где – векторные проекции векторов на площадку с нормалью  , определяемую (5), – орт касательной к этой площадке.

Формулы (7) есть другое выражение закона Гука (1), только записанного на равнонаклонных к осям 1, 2, 3 площадках. Здесь усилия по направлениям и вызывают относительные смещения только в направлении «своего» действия.

Поскольку в (7) ничего не говорится о том, какие по величине должны быть нормальные деформации в поперечном направлении под действием усилий , то именно в этом месте возможно принять такую гипотезу: все первоначально изотропные материалы состоят из жестких недеформируемых частиц­ – блоков, образованных пересечением равнонаклонных к осям 1, 2, 3 площадок или плоскостей, по нормали к которым происходит такой вид деформации как простое удлинение (рис. 3 а), по касательной – простой сдвиг (рис. 3 б).

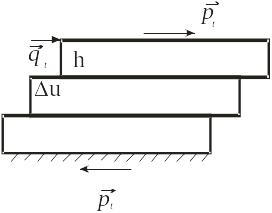
а б

Рис. 3. Два простейших вида деформации, лежащие в основе образования произвольной деформации произвольного по структуре тела: а – простое удлинение; б – простой сдвиг

То что блоки жесткие (недеформируемые), означает то, что в поперечном направлении усилия вообще никаких деформаций не вызывают (эффект Пуассона отсутствует!). С другой стороны, жесткость блоков означает еще и то, что плоскости скольжения блоков (или контактные площади), определенные в упругости, остаются таковыми же плоскостями скольжения при неупругом деформировании первоначально изотропной среды. Данная гипотеза связывает упругое и неупругое поведения среды. Поэтому справедливость ее будет доказана, если предсказанные упругостью определяющие соотношения пластичности и разрушения будут экспериментально подтверждены.

Поскольку речь идет о блоках, о блочной системе, то здесь же ставится вопрос о размерах самих блоков, и межблочного пространства, вопрос о том, где эта информация хранится. В завуалированном виде она хранится в константах упругости , и других характеристиках среды, отражающих в том числе ее неупругие свойства. Покажем это на примере определения константы . Для этого рассмотрим разрез блочной структуры, представленный на схеме рис. 3 а. Обозначим высоту одного блока как , толщину межблочного пространства как , площадь основания блока, к которому приложена внешняя сила , как , площадь межблочного пространства как . Пусть – модуль Юнга материала межблочного пространства. Так как рассматриваемый элемент среды находится в равновесии, то это означает в силу справедливости закона Ньютона, что к каждому его горизонтальному сечению будут приложены две силы: и . Эти силы вызовут изменение расстояния между блоками за счет растяжения или сжатия податливой прослойки между блоками. Пусть – изменение расстояния для одной такой прослойки. Тогда в силу того, что по вертикали она деформируется упруго, имеем

,

где – нормальное напряжение на площадке с нормалью , определяемой (4). Так как сами блоки жесткие, то . Складывая все изменения в размерах высот рассматриваемой блочной системы, получаем

,

где – число блоков в системе на рис. 3 а, – число прослоек. Так как первоначальная длина равна

,

то отсюда находим

и соответственно модуль в виде

. (7)

В этой формуле . Из нее видно то, что не совпадает с модулем Юнга для одной прослойки, зависит как от отношения размеров блоков и межблочного пространства, так и от отношения площадей этих блоков, т. е. вся информация о блочной структуре здесь имеется.

В связи с (7) сделаем замечание. Константа связывается известным образом со скоростью распространения продольной волны. Если допустить, что ее значение через скорость известно, то формулу (7) возможно использовать для определения, например, размера блока, зная размер межблочного пространства. Если знать , то эту формулу возможно использовать для определения модуля Юнга прослойки .

Несколько слов о сдвиге одних блоков относительно других. Следует отметить, что сдвиг предполагает действие двух нагрузок – одной нагрузки сдвигающей, другой – прижимающей (или отталкивающей) блоки друг к другу. Понятно то, что при наличии трения между блоками здесь существенную роль играет порядок приложения указанных нагрузок, от которого зависит работа, совершаемая этими силами, величина сдвига. Чтобы избежать неудобства, вызванного слежением за порядком действия нагрузок, можно допустить, что блоки еще в ненагруженном состоянии были прижаты и остаются прижатыми друг к другу при нагружении за счет некоторого усилия , обусловленного, например, поверхностными силами натяжения и другими силами (межатомными, межмолекулярными и т. д.), так, что суммарное нормальное напряжение между ними есть . Тогда усилие трения, необходимое для напряжения всевозможных неровностей на контактных площадках и перескока одних из них через другие, есть

, (8)

где – коэффициент трения. Очевидно, что коэффициент трения зависит от смещения одного блока относительно другого, причем . От угла зависит также периметр фигуры на рис. 3 б, от которого в свою очередь зависит сила натяжения . Если в (8) допустить, что , то есть значением по сравнению с можно пренебречь, тогда справа в (8) будет стоять функция сдвига (при фиксированном  !), которая раскладывается в ряд по степеням . В зависимости от значений и количества сохраняемых слагаемых будем иметь линейную, нелинейную (кубическую) функцию и т. д., что отвечает упругому, неупругому деформированию и т. д. [2].