2.4.4. Коэффициент детерминации

Коэффициент детерминации равен квадрату множественного коэффициента корреляции и применительно к корреляционному анализу показывает: какую долю общей дисперсии исследуемого показателя Xj объясняет (формирует) вариация всех остальных (n-1) показателей X₁,X₂,…,X_n при их совместном действии:

(2.14)

2.4.5. Оценка значимости множественного коэффициента детерминации

Используется F – статистика Фишера для R²:

(2.15)

где, n – число компонент вектора ; N – число опытов.

Проверяется нуль гипотеза:

H₀ : F = 0;

если то коэффициент множественной корреляции незначим (гипотеза Н₀ принимается);

если то R² значим (гипотеза Н₀ отвергается);

n₁– число степеней свободы для числителя; n₂ – число степеней свободы для знаменателя (n₁=n-1; n₂=N-n) дроби (2.15).

2.4.6. Индекс корреляции при нелинейной связи двух случайных величин

Слово «индекс» здесь понимается в смысле «отношения» [1]. Поэтому употребляется и другой термин для этой числовой меры: «корреляционное отношение».

Пусть две случайные величины X и Y связаны в среднем нелинейным функциональным уравнением вида:

(2.16)

Пример:

Функция f(x) должна быть априори известна.

(2.16)

Тогда выборочная оценка индекса корреляции равна:

(2.17)

Практическая формула для индекса корреляции [ ]:

(2.18)

Здесь:

– дисперсия остатков уравнения регрессии;

– общая дисперсия как мера разброса наблюдений вокруг среднего.

Заметим, что при подстановке и под корень в уравнении (2.18) и условии (N-n)»(N-1) при больших N степени свободы и их можно сократить, откуда следует упрощенная приближенная расчетная формула:

(2.20)

Эта формула допускает наглядное толкование: чем сильнее стохастическая связь в уравнении (2.16), тем меньше доля дисперсии по отношению к общей дисперсии и больше индекс корреляции .

2.4.7. Индекс множественной корреляции

Пусть построено нелинейное по независимым переменным уравнение множественной регрессии:

(2.20)

Тогда использую простую формулу (2.20), можно получить индекс множественной корреляции

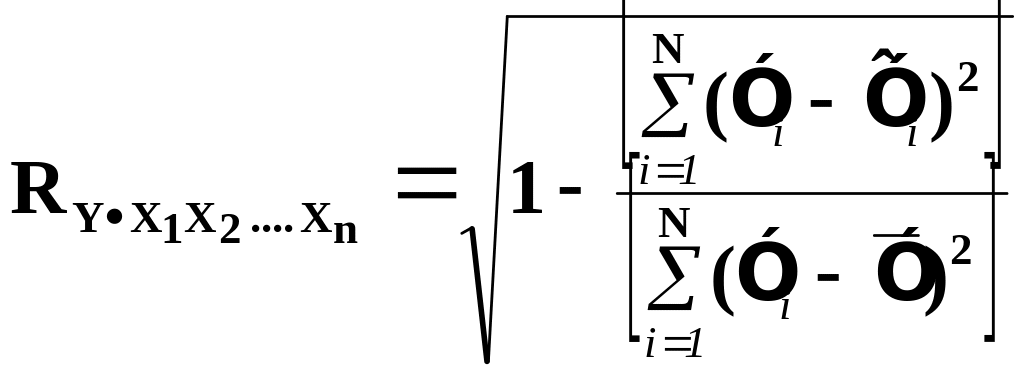(2.21)

Соответственно квадрат этого индекса даст множественный индекс детерминации в нелинейном случае.

2.5. Коэффициент ранговой корреляции

Коэффициент ранговой корреляции служит числовой мерой стохастической связи между качественными (нечисловыми) показателями

Качественные показатели называют также ординальными и порядковыми переменными.

Пример:

На соревнованиях по фигурному катанию получена таблица оценок за «технику» g_i и «артистичность» y_i (два качественных признака).

Номер оценки	Ранги
	оценка за «технику» признак g	оценка за «артистичность» признак y
i	gi	yi
1	g1	y1
2	g2	y2
….	….	….
N	gN	yN

Здесь g_i, y_i – ранги (баллы), т.е. значения ординальных переменных, которые находятся путем экспертных оценок (оценки судей).

Выборочная оценка, коэффициента ранговой корреляции Спирмена определяется по формуле

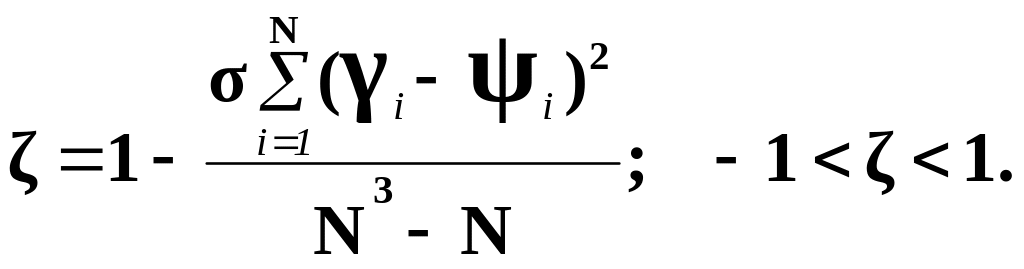(2.22)

N – число наблюдений (строк).

Значимость коэффициента ранговой корреляции Спирмена проверяется аналогично (2.9) по критерию Стьюдента.