3.6.7. Проверка гипотезы о нормальном законе распределения остатков

Обычно используется (R/S) - критерий, т.е. нормированный размах остатков:

(R/S) = (е_max-е_min)/S_e, (3.34)

где S_e определяется формулой (3.20).

Вывод:

Если , то гипотеза о нормальном законе распределение остатков {е_i} не отвергается.

В противном случае – отвергается.

Общий вывод: Если все 6 гипотез, рассмотренные выше, о предпосылках метода наименьших квадратов выполняются и критерий качества модели R² приемлем для поставленных целей моделирования, то модель считается адекватной и пригодной для практического применения.

Замечание. Если выборка деформируется (сужается или расширяется) либо изменяется принимаемый уровень значимости a оценок, то проверку адекватности надо делать заново.

3.7. Точечный прогноз и оценка доверительных интервалов прогноза

Найдем средние квадратические отклонения, которые потребуются нам при получении полуширины доверительных интервалов прогноза для:

• коэффициентов регрессии ;

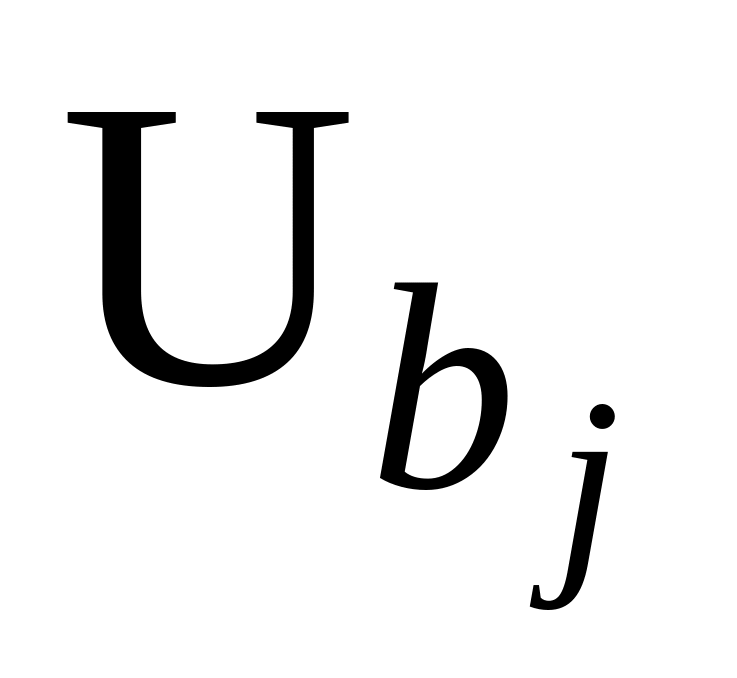• расчетного значения моделируемой величины ;

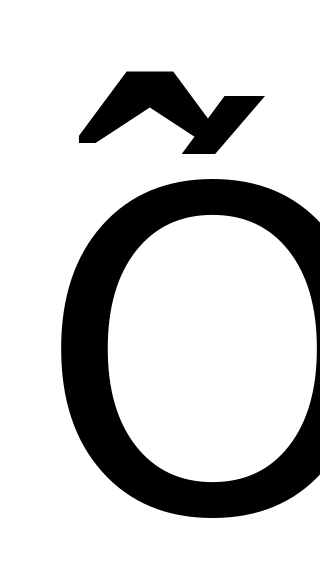
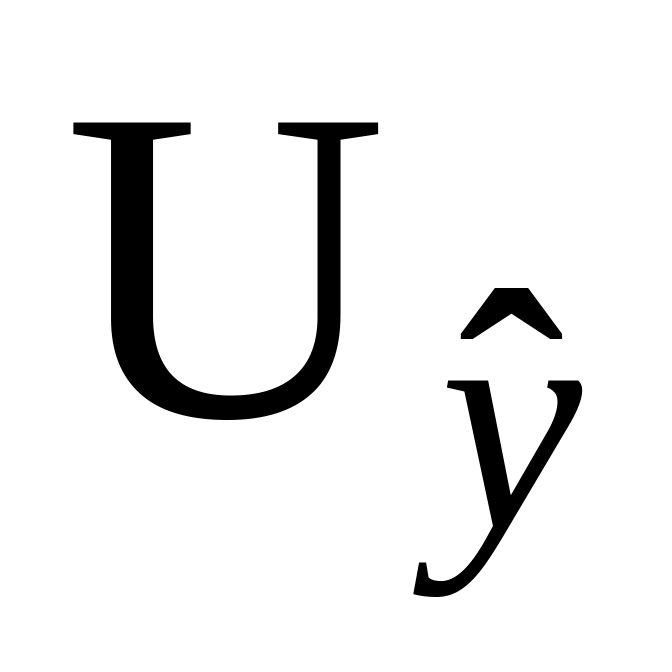• индивидуальных значений 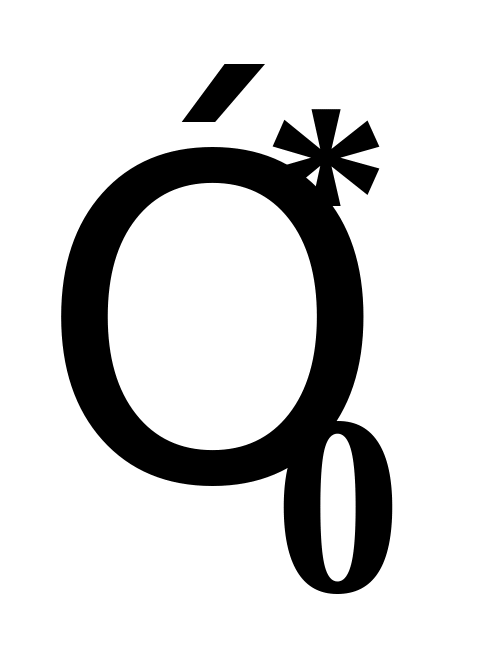случайной величины Y

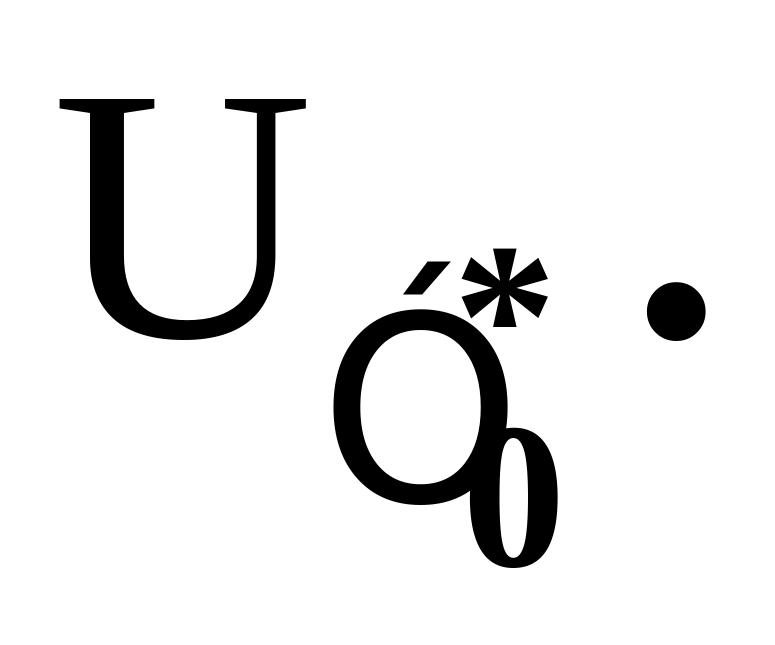
1) Среднее квадратичное отклонение наблюдений относительно срединной поверхности регрессии ( в одномерном случае – относительно линии регрессии ), находиться по формуле (3.20).

2) Среднее квадратическое отклонение для случайных величин – коэффициентов регрессии :

(3.35)

Здесь – диагональный элемент с номером строки j в информационной матрице Фишера.

3) Среднее квадратическое отклонение расчетного значения :

(3.36)

где – значение вектора регрессоров в точке прогноза; «Т» – знак транспортирования.

4) Среднее квадратическое отклонение для индивидуальных значений случайной величины Y в точке прогноза :

(3.37)

5) Полуширина доверительного интервала :

(3.38)

6) Полуширина доверительного интервала :

(3.39)

7) Полуширина доверительного интервала для разброса индивидуальных значений Y:

(3.40)

3.8. Оценка погрешностей расчета по уравнению регрессии

Традиционно используются две числовые меры для оценки погрешностей расчета:

• Среднеквадратическая ошибка S_e по формуле (3.20).

• Средняя по модулю относительная ошибка.

(3.41)

Замечание: Числовые меры ошибок расчета S_e по (3.20) и по (3.41) оценивают точность модели внутри области эксперимента, где мы имеем информацию о поведении моделируемой зависимости . Более важной является информация о погрешности расчета в области прогноза, где никаких наблюдений нет. В этом аспекте более информативна оценка погрешности расчета по данным ретроспективного анализа.

Идея заключается в следующем. Пусть имеется многомерная выборка из N наблюдений, упорядоченных во времени. При оценке вектора параметров в уравнении регрессии (3.6) будем пользовать не все N точек базы данных, а только N₁ точек. Оставшиеся N-(N₁+1) точек используются для объективного ретроспективного тестирования модели, ибо в этих точках мы знаем и экспериментально измеренные значения и расчетные значения (i= N₁+1,…,N).

Получим оценки погрешности:

• среднеквадратичную

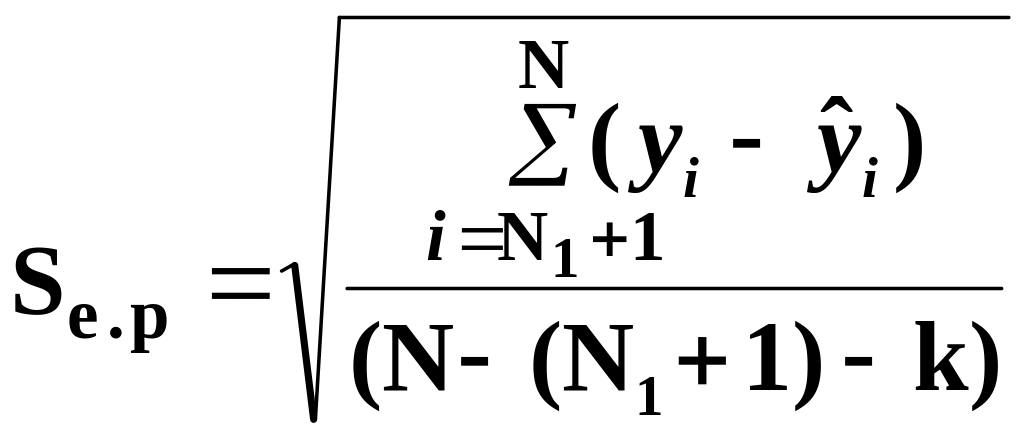(3.42)

• среднюю по модулю

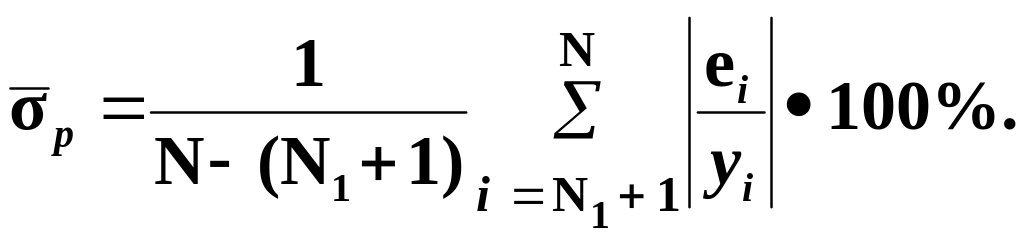(3.43)