20 Признак Даламбера сходимости ряда с положительными членами.

Пусть дан ряд с положительными членами, для которого существует предел отношения последнего члена ряда к первому:

ρ = lim a_n+1/a_n

^n->∞

Справедливо:

• если ρ<1, то ряд сходится

• если ρ>1, то ряд расходится

Доказательство:

Воспользуемся тем, что сходимость не зависит от конечного чилса слагаемых ряда.

1) При любом ε>0:

ρ - ε ≤ a_n+1/a_n ≤ ρ + ε (*)

Пусть ρ<1

ε можно выбрать настолько малым, что ρ + ε < 1, тогда, начиная с какого-то номера:

a_n+1 ≤ (ρ + ε) a_n

a_n+2 ≤ (ρ + ε) a_n+1

Если истинно предыдущее высказывание, получаем:

A_n+k ≤ (ρ + ε) a_n

A_Nε+k ≤ (ρ + ε) a_n

k=1,2…

Таким образом, все члены ряда, начиная с Nε, не превосходят геометрической прогрессии с q<1. То есть по теореме сравнения ряд сходится, и утверждение 1 верно.

2) Пусть ρ>1

Выберем настолько малое ε, что ρ - ε > 1. Тогда:

a_n-1 ≥ (ρ – ε) a_n

Из этого следует, что последующий член будет больше предыдущего, и общий член ряда не может стремится к 0. Ряд расходится по необходимому признаку сходимости.

21. Радикальный признак Коши сходимости ряда с положительными членами

Теорема:

Пусть дан ряд с положительными членами, для которого существует конечный предел корня n-ой степени из n-ого члена.

Справедливы утверждения:

l<1 -> ряд сходится

l>1 -> ряд расходится

Док-во:

Доказательство основано на сравнении данного ряда с рядом, составленным из членов геометрической прогрессии.

Начиная с некоторого номера справедливы неравенства:

1. Предположим, l<1, l+эпсилон<1

Тогда, начиная с некоторого номера справедливо неравенство

Поскольку ряд геометрической прогрессии сходится, то сходится и наш ряд.

2. Предположим l>1, l-эпсилон>1

Тогда, начиная с некоторого номера справедливо неравенство

Поскольку ряд геометрической прогрессии расходится, то расходится и наш ряд.

Пример.

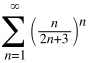
22. Интегральный признак сходимости ряда с положительными членами

Теорема:

Пусть дан ряд с положительными членами

Предположим, что выполнены 2 условия:

• Члены ряда монотонно убывают с ростом n (a1>a2>…>an>…)

• Существует монотонно-убывающая функция y=f(x), которая является непрерывной, и ее значение при целых значениях x совпадают с величинами, соответствующих членов ряда (f(n)=an)

Тогда справедливы следующие утверждения:

• Если интеграл

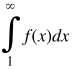
сходится, то и ряд сходится.

• Если расходится, то и ряд тоже расходится.

Док-во:

Рассмотрим график функции y=f(x) и изобразим на комплексной плоскости величины членов ряда в виде точек на этом графике.

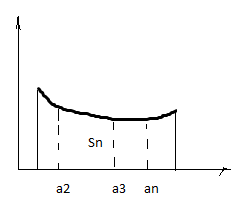
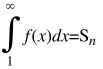
Можно рассмотреть две фигуры, которые являются ступенчатыми, и одна из них будет входить в криволинейную трапецию, а вторая выходить за ее пределы.

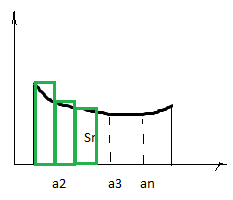
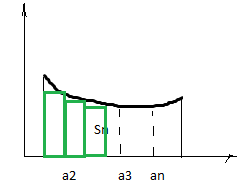
Обозначим площади входящей и выходящей фигур

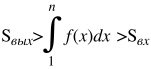
Из рисунка видно, что 

Таким образом:

Тогда существует предел:

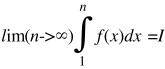
При предельном переходе неравенство сохраняется, поэтому мы получаем, что

 

следовательно

Частичные суммы ограничены сверху, следовательно ряд сходится.

Из сходимости интеграла вытекает сходимость ряда.

Предположим что ряд расходится. Тогда справедливо неравенство:

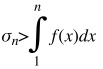
Поскольку интеграл сходится, то

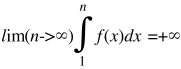
А в силу предыдущего неравенства sigma_n будут неограниченными по n, т.е ряд будет также расходится.

23. Теорема о равносходимости рядов с положительными членами

Существует эталонный ряд, который называется рядом Дирихле, сходимость или расходимость которого устанавливается с помощью интегрального признака, и этот ряд позволяет установить сходимость или расходимость очень большого количества рядов, равносходящихся с этим рядом.

Рядом Дирихле называется следующий ряд:

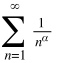
Применим к этому ряду интегральный признак.

В данном ряде достаточно рассмотреть случай, когда α>0

Рассмотрим функцию:

Рассмотрим интеграл:

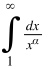
Если α>1 интеграл сходится, если α≤1 интеграл расходится.

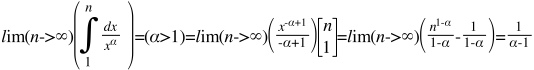
Те же выкладки можно использовать и для случая α<1.

Поскольку 1-α>0, то первый член под знаком предела будет неограниченно расти, т.е интеграл будет расходящимся, следовательно и ряд тоже будет расходящимся.

Случай α=1 нужно рассматривать отдельно.

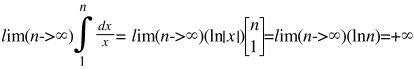
Таким образом мы можем написать, что ряд Дирихле при α>1 сходится, а при α≤1 расходится.

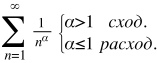
При α=1 ряд расходится:

Ряд Дирихле играет важную роль, поскольку с его помощью и с помощью теоремы о равносходимости можно устанавливать сходимость или расходимость целого ряда других рядов.

Пример №1:

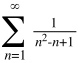
Члены ряда - a_n

Будем сравнивать этот ряд с рядом Дирихле:

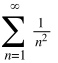
Члены ряда - b_n

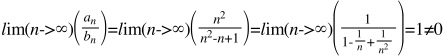
По теореме о равносходимости два ряда сходятся одновременно.

Поскольку второй ряд сходится, то сходится и первый.

Пример №2:

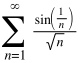
Числитель с ростом n стремится к нулю. Заменим sin(1/n) на 1/n

Сравним этот ряд с рядом:

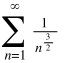
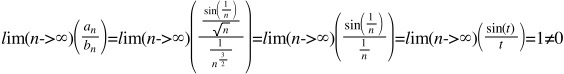
Следовательно, ряды равносходящиеся.

Поскольку второй ряд сходится, то и первый сходится.

24. Понятие остатка ряда. Задача вычисления суммы ряда с данной точностью

Ряд, полученный отбрасыванием от исходного n первых членов, называется n-м остатком ряда.

Обозначение:

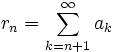
Все члены, кроме тех, что входят в n-й остаток ряда, в сумме дают т. н. n-ю частичную сумму ряда.

Свойства

Для остатка ряда справедливы следующие утверждения:

• Если ряд сходится, то сходится любой его остаток.

• Если хотя бы один остаток ряда сходится, то и сам ряд сходится.

• Если ряд сходится, то

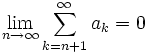
Задача вычисления суммы ряда с данной точностью означает найти такое число X, для которого выполняется неравенство |X-Y| < eps, где Y - сумма ряда (найденная аналитически), а eps - заданная точность.