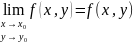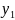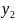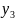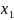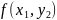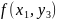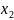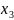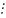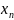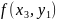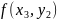- •Понятие функции нескольких аргументов. Способы задания. Понятие о линиях и поверхностях уровня.
- •Предел в точке для функции нескольких аргументов. Непрерывность.
- •Понятие частной производной функции нескольких аргументов.
- •Дифференцируемость функции нескольких аргументов. Полный дифференциал. Линеаризация функции.
- •5 Нахождение частных производных сложных функций. Частные производные сложной функции нескольких переменных
- •Неявные функции одной и двух переменных. Нахождение производных неявных функций.
- •7. Частные производные и дифференциалы высших порядков.
- •8. Понятие локального экстремума функции нескольких аргументов. Необходимые условия экстремума. Стационарная точка.
- •9.Достаточные условия локального экстремума функции нескольких аргументов.
- •10.Определение и теорема существования двойного интеграла.
- •11.Свойства двойного интеграла.
- •12. Геометрический смысл двойного интеграла.
- •17. Поверхностная и объёмная плотность. Нахождение массы по известной плотности с помощью двойных и тройных интегралов.
- •18 Числовые ряды. Сходимость и расходимость. Необходимый признак сходимости ряда.
- •19 Ряды с положительными членами. Теорема сравнения.
- •20 Признак Даламбера сходимости ряда с положительными членами.
- •25.Знакочередующиеся ряды. Теорема Лейбница. Задача вычисления суммы знакочередующегося ряда с данной точностью.
- •34 Тригонометрический ряд. Ряд Фурье данной периодической функции.
- •35 Теорема о сходимости ряда Фурье для кусочно-гладкой периодической функции.
- •36 Разложение в ряд Фурье четных и нечетных функций. Разложение по синусам или по косинусам на полупериоде.
- •Ряд Фурье на полупериоде.
- •37 Ряды Фурье для периодических функций с произвольным периодом.
- •38 Понятие функции комплексной переменной. Расширение в комплексную область элементарных функций.
- •Основные элементарные функции комплексного переменного
- •Рациональная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция – функция, обратная показательной.
- •39 Ряды с комплексными членами. Степенные ряды в комплексной области
- •45. Теорема о дифференцировании оригинала
- •46. Теорема об интегрировании оригинала.
- •Понятие свертки двух оригиналов. Теорема о свертке.
- •Решение обратной задачи операционного исчисления для рациональных изображений.
- •Операционный метод решения линейных дифференциальных уравнений и систем с постоянными коэффициентами.
Понятие функции нескольких аргументов. Способы задания. Понятие о линиях и поверхностях уровня.
ОПР. Функцией нескольких аргументов называется закон соответствия, сопоставляющий каждой совокупности значений аргументов некоторое число, т.е., если всем аргументам придать какое-нибудь значение, то получим n-мерный вектор и функция является законом соответствия, где каждому вектору соответствует значение функции
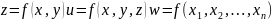
Способы задания
Аналитический
Графический
Табличный
Аналитический способ задания функции с помощью формулы. Он может быть применен для задания функции любого числа аргументов.
При графическом способе функция 2х аргументов задаётся с помощью поверхности, которая находится в пространстве и расположена относительно системы координат так, что любая прямая параллельная оси Z пересекает поверхность в одной точке.

z=f(x, y)

z=f(x,y)

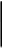

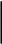


y
x
Можно однозначно спроектировать фигуру на плоскость XOY. Заметим, что для функции 2х аргументов, если она задана, например, аналитически, можно построить график, а именно, через каждую точку с координатами (x,y)провести прямую, параллельную оси Z и на ней отложены значения функции, тем самым получим точку. Если это сделать для всех точек определённой фигуры, то получим множество точек, которое как правило состоит некоторую поверхность, эта поверхность и называется графиком функции.
Табличный способ. В случае, когда функция 2х аргументов определена экспериментально и в результате каких-либо вычислений функцию задают в виде таблицы с 2мя входами z=f(x,y)
x\y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция задаётся аналитически, то множество всех n-мерных точек, для каждой из которых выражение из функции называется естественной областью определения. Для функции 2х аргументов часто используется понятие линии уровня функции.
f(x,y)=C Константу C можно менять, т.е. получить семейство уравнений.
f(x,y,z)=C При различных С получим семейство поверхностей уровня.
Гиперповерхность
уровня, т.е. множество точек в n-мерном
пространстве, для которых выполняется
равенство f(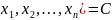
Предел в точке для функции нескольких аргументов. Непрерывность.
z=f(x,y)
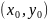 -выколотая
окрестность, функция f(x,y)
определена.
-выколотая
окрестность, функция f(x,y)
определена.
Опр.
Число А называется пределом функции
f(x,y)в
точке
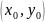 ,
если для любой последовательности точек
,
если для любой последовательности точек
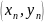 (придумай слово сам) окрестности такой,
что
(придумай слово сам) окрестности такой,
что
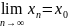
 справедливо равенство
справедливо равенство
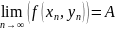 .
В данном определении важный момент
состоит в том, что последовательность
точек является произвольной, при этом
предел значений последовательности
функции должен быть один и тот же. Если
для одной последовательности, а для
другой –нет, то говорят, что в точке
функция не имеет предела.
.
В данном определении важный момент
состоит в том, что последовательность
точек является произвольной, при этом
предел значений последовательности
функции должен быть один и тот же. Если
для одной последовательности, а для
другой –нет, то говорят, что в точке
функция не имеет предела.
Непрерывность функции нескольких аргументов.
Функция 2х аргументов z=f(x,y) называется непрерывной в точке выполняются следующие 3 условия
Функция определена в точке
В точке существует предел функции
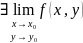
Предел функции в данной точке совпадает со значением функции в этой точке