МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Кемеровский государственный университет»

Кафедра ЮНЕСКО по новым информационным технологиям

С.Ю. Завозкин Информатика

Лабораторный практикум

Кемерово, 2011

УДК 004.5, 004.77

Информатика. Лабораторный практикум. / С.Ю. Завозкин – Кемерово, КемГУ, 2011.

Оглавление

Оглавление 3

Лабораторная работа 1. Системы счисления, формы представления чисел 4

Лабораторная работа 2. Представление чисел в ЭВМ, кодирование 11

Лабораторная работа 3. Логические основы алгоритмизации 20

Лабораторная работа 4. Алгоритмы 30

Лабораторная работа 1. Системы счисления, формы представления чисел

1. Цель работы

Изучить системы счисления и формы представления чисел. Получить навыки по работе с различными системами счисления, по переводу из одной системы счисления в другую, а также по представлению числе в нормализованном виде.

2. Теоретический материал

Система счисления – это способ наименования и изображения чисел с помощью цифр, то есть символов, имеющих определенные количественные значения.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. Основанием системы счисления называется количество различных цифр, используемых для изображения числа в позиционной системе счисления. Позицией называется место каждой цифры в числе.

Перевод целых чисел из одной системы счисления в другую в общем случае осуществляется по следующим правилам.

Правило 1. Перевод числа x из системы счисления основанием P в систему счисления с основанием Q заключается в последовательном нахождении остатков от деления числа x на основание Q, при этом процесс продолжается до тех пор, пока частное от деления не будет меньше основания Q. Все вычисления выполняются в системе счисления с основанием P, т.е. основание Q должно также быть выражено в системе счисления с основанием P.

Остатки от деления должны быть выражены цифрами системы счисления с основанием Q. Представление искомого числа в системе счисления с основанием Q получается выписыванием последнего частного и остатков от деления в обратном порядке.

Правило 2. Перевод числа x из системы счисления основанием P в систему счисления с основанием Q осуществляется путем представления числа х по степеням основания P. Все вычисления выполняются в системе счисления с основанием Q, т. е. основание P и цифры исходного числа должны также быть выражены в системе счисления с основанием Q.

На практике такой порядок перевода чисел используется при переводе десятичную систему счисления.

23Е₁₆ = ?₁₀ = 2*16²+3*16¹+ Е*16⁰ = 574₁₀

1078₈ = 1*8³+0*8²+7*8¹+6*8⁰ = 574₁₀

Правило 3. Перевод чисел из восьмеричной системы счисления в двоичную и наоборот переводится по Триадам.

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
000	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7

Правило 4. Перевод чисел из шестнадцатеричной системы счисления в двоичную и наоборот переводится по тетрадам. Пример, 23E₁₆ = 0010 0011 1101₂

Далее представлены примеры перевода целых чисел из одной системы счисления в другую.

Двоичная система счисления:

110011₂= 1*2⁰+1*2¹+0*2²+0*2³+1*2⁴+1*2⁵ = 51₁₀

_{11012= 1*23 + 1*22+0*21+ 1*20 = 1310}

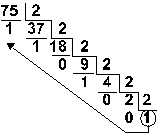
7510 = 1 001 0112

Восьмеричная система счисления:

341₈ =3*8²+ 4*8¹ +1*8⁰ = 225₁₀

1076₈ = 1*8³+0*8²+7*8¹+6*8⁰ = 574₁₀

1076₈ = 001 000 111 110₂ (перевод по триадам)

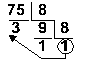
7510 = 1138

Шестнадцатеричная система:

A1F₁₆ = A*16² + 1*16¹ + F*16⁰ = 2591₁₀

23Е₁₆ = 2*16²+3*16¹+ Е*16⁰ = 574₁₀

23E₁₆ = 0010 0011 1101₂ (перевод по тетрадам)

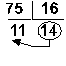
7510 = 4B16

Перевод дробных чисел из одной системы счисления в другую

Как правило, это происходит через промежуточный перевод в десятичную систему: ; .

Шаг 1

Если основание СС – p, простая дробь содержит n цифр и b_k – цифры дроби (1 ≤ k ≤ n, 0 ≤ b_k ≤ p^-1), то она может быть представлена в виде суммы:

O,Y_p = ∑ b_k p^-k

Пример: 0,011₂ =0*2^-1+1*2^-2+1*2^-3=0,375₁₀

Шаг 2

1. Умножить исходную дробь в десятичной СС на p, выделить целую часть – она будет первой цифрой новой дроби, отбросить дробную часть;

2. Для оставшейся дробной части операцию умножения с выделением целой и дробной частей повторять, пока в дробной части не останется 0, или не будет достигнута желаемая точность. Появляющиеся при этом целые будут цифрами новой дроби;

3. Записать дробь в виде последовательности цифр после ноля с разделителем в порядке их появления в п.1 и 2.

Пример:

0,375₁₀→ O,Y₂

0, 375*2 = 0, 750

0, 75*2 = 1, 50

0, 5*2 = 1 , 0

0,375₁₀ = 0,011₂

Формы представления чисел

• С фиксированной точкой (естественная форма).

• С плавающей точкой (нормализованный вид).

С фиксированной точкой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной. Например, 0,25; -10,44; +0,9781.

Число Х₁₀ называется нормализованным, если оно представлено в виде Х₁₀ =±М₁₀*10^±К, где М₁₀ – мантисса, 0,1≤ М₁₀< 1, К-порядок, целое положительно десятичное число.

Например: -1234₁₀= -0,1234*10⁴, 0,003=0,3*10^-2

При нормализации выполняется деление числа на 4 составляющих: знак числа, мантисса, знак порядка, порядок.

Для произвольной системы счисления Х_р =± М_р*P^±К , Р^-1 ≤ М< 1.