2.3.2.Запись натурального числа в двоичной системе
Примером
двоичного кода является запись
натурального числа
в позиционной
системе счисления с основанием 2
Пусть
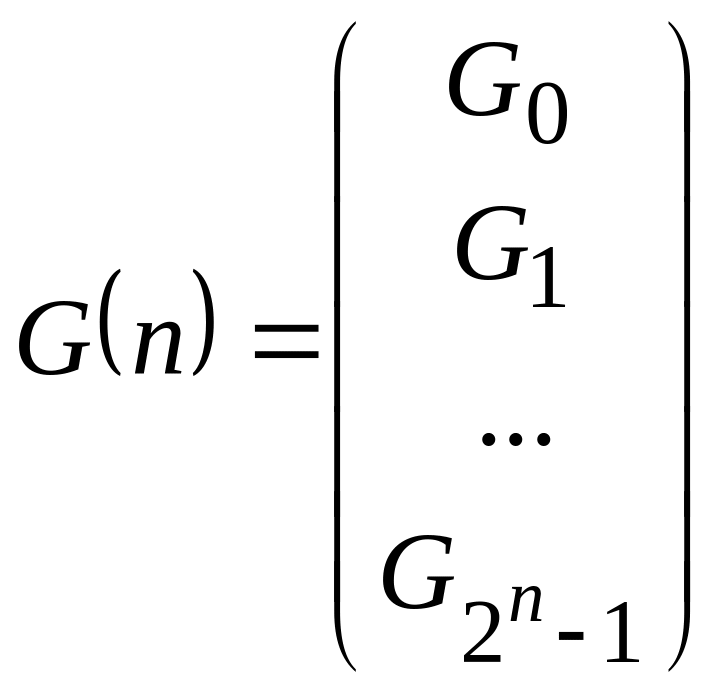- последовательность
двоичных кодовых слов длины
.
Тогда рекурсивное
определение последовательности кодовых
слов в порядке двоичного счета будет
следующее:
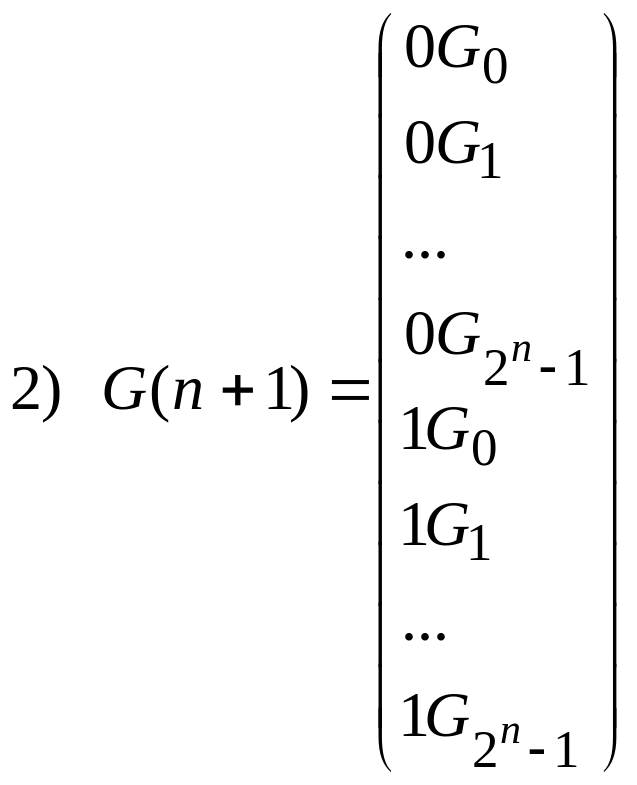
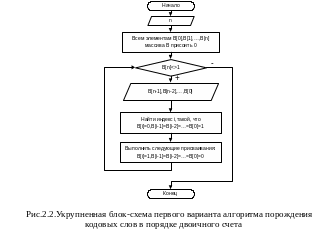
Наиболее прямым способом порождения данной последовательности кодовых слов является счет в системе счисления с основанием 2, что реализует алгоритм, представленный укрупненной блок-схемой на рис.2.2.
Укрупненная блок-схема показывает идеи алгоритма и не расскрывает многие детали реализации. В рассматриваемом алгоритме из укрупненной блок-схемы видно, что двоичные наборы длины n формируются в ячейках B[n-1],B[n-2],...,B[0], массива B. Ячейка B[n] массива B служит для организации завершения работы алгоритма. Ячейка B[n] принимает значение 1, когда все 2n наборов выданы. Также видно, что для реализации двоичного счета, т.е. для организации перехода от текущего кодового слова к следующему, используется простой прием:
просматривается текущее кодовое слово в направлении от младшего разряда к старшему, с целью поиска первого разряда равного нулю (на укрупненной блок-схеме номер такого разряда сохраняется в переменной i);.
найденному первому разряду равному нулю присваивается значение 1, а все «более младшие» разряды, значение которых равно 1, обнуляются.
Укрупненная блок-схема показывает идеи алгоритма и не расскрывает многие детали реализации. В рассматриваемом алгоритме из укрупненной блок-схемы видно, что двоичные наборы длины n формируются в ячейках B[n-1],B[n-2],...,B[0], массива B. Ячейка B[n] массива B служит для организации завершения работы алгоритма. Ячейка B[n] принимает значение 1, когда все 2n наборов выданы. Также видно, что для реализации двоичного счета, т.е. для организации перехода от текущего кодового слова к следующему, используется простой прием:
просматривается текущее кодовое слово в направлении от младшего разряда к старшему, с целью поиска первого разряда равного нулю (на укрупненной блок-схеме номер такого разряда сохраняется в переменной i);.
найденному первому разряду равному нулю присваивается значение 1, а все «более младшие» разряды, значение которых равно 1, обнуляются.
Однако из укрупненной блок схемы не видны детали реализации перехода от текущего кодового слова к следующему. Обычно подобная детализация не вызывает трудностей.
В некоторых случаях будем приводить детальные блок-схемы алгоритмов и (или) реализацию алгоритмов на языке Pascal. Поскольку алгоритма порождения кодовых слов в порядке двоичного счета является первым, рассматриваемым нами алгоритмов, то приведем его детальную блок-схему и программную реализацию. Детальная блок-схема алгоритма представлена на рис. 2.3, программная реализация представлена листингом 2.1.
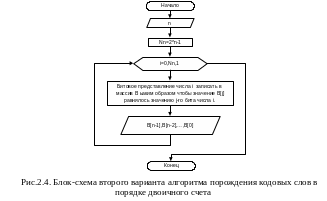
Еще один способ порождения последовательности кодовых слов в порядке двоичного счета заключается в переборе всех целых чисел от 0 до 2n-1 и обращением двоичного представления каждого из чисел в набор (bn-1,bn-2,...,b0). Обращение осуществляется с помощью битовых операций или с помощью операций целочисленного деления и получения остатка от деления. Укрупненная блок схема алгоритма реализующего данный подход показана на рис.2.4. Одна из возможных программных реализаций представлена в листинге 2.2.
Листинг 2.1
const n_max=50; {максимальная длина кодового слова}
var B:array[0..n_max] of byte;
i,n:byte;
begin
write(‘Введиде длину кодового слова n=’); readln(n);
for i:=0 to n do B[i]:=0;
while B[n]<>1 do
begin
for i:=n-1 downto 0 do write(b[i]); writeln;
i:=0;
while B[i]=1 do
begin
B[i]:=0;
i:=i+1
end;
B[i]:=1
end;
end;
Листинг 2.2
const n_max=50; {максимальная длина кодового слова}
var B:array[0..n_max] of byte;
Nn,k,i:word;
j:byte;
begin
write(‘Введиде длину кодового слова n=’); readln(n);
Nn:=1;
for j:=1 to n do Nn:=Nn*2;
Nn:=Nn-1;
for i:=0 to Nn do
begin
k:=i;
for j:=0 to n-1 do
begin
B[j]:=k mod 2;
k:=k div 2
end;
for j:=n-1 downto 0 do write(b[j]); writeln;
end;
end;