7.5.2.Алгоритм расчета наиболее поздних сроков наступления событий
Проанализируем сетевой график, с целью определения для каждого события x наиболее поздний срок его наступления L(x), т.е. срок появления события x, еще допускающий своевременное окончание всего проекта.
Рассмотрим фрагмент некоторого сетевого графика, представленный на рис.7.24. Пусть известны наиболее поздние сроки наступления 20,24 и 29 события и эти сроки соответственно равны 16, 19 и 22 единицам времени. Другими словами, если событие 20 наступит через 16 единиц времени после начала работы над проектом, то еще можно в намеченный срок завершить весь проект. Если же событие 20 наступит по прошествии более 16 единиц времени от начала работы над проектом, то это приведет к задержке выполнения проекта. Аналогично, если 24 или 29 событие наступят соответственно по прошествии 19 и 22 единиц времени от начала работы над проектом, то это также приведет к задержке выполнения проекта.
Требуется рассчитать наиболее поздний срок наступления события 17. Очевидно, что событие 17 не может произойти позже, чем через L(20)-t(17,20)=16-5=11 единиц времени после начала работы над проектом. Кроме того, событие 17 не может произойти позже, чем L(24)-t(17,24)=19-4=15 единиц времени, иначе событие 24 наступит слишком поздно, (более 19 единиц времени). Также событие 17 не может произойти позже, чем L(29)-t(17,29)=22-8=16 единиц времени, иначе событие 29 наступит слишком поздно, (более 22 единиц времени).
Таким образом, наиболее ранний срок наступления события 17 равен min(11,15,16)=11 единицам времени.
В общем случае наиболее поздний срок события i в сетевом графике G=(V,E) рассчитывается по формуле:
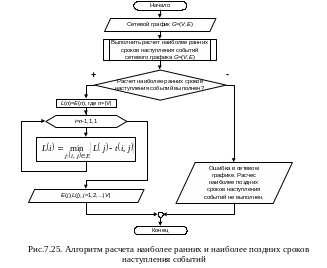
Алгоритм расчета наиболее поздних сроков наступления событий представлен на рис.7.25.
Реализация алгоритма расчета наиболее поздних сроков наступления событий приведена в листинге 7.13.
Листинг 7.13
Здесь должно быть описание констант, типов, переменных и функций EDuga, TopSort, RaschetE из листинга 7.12.
{ Функция RaschetEL выполняет расчет наиболее ранних и наиболее поздних сроков
наступления событий сетевого графика заданного матрицей весов T размера N на N.
Возвращает true, если расчет выполнен и false, в противном случае (сетевой график задан
неверно, содержит контур).
Если расчет наиболее ранних и наиболее поздних сроков наступления событий выполнен,
то данные сроки сохраняются в выходных массивах E и L соответственно.
E[i] - наиболее ранний срок наступления i-го события,
L[i] - наиболее поздний срок наступления i-го события.}
function RaschetEL(T:tGraf; N:integer; var Num:tNum; var E,L:tEl):boolean;
var i,j:integer;
begin
if not RaschetE(T,N,Num,E) then RaschetEL:=false {Расчет наиболее ранних сроков
наступления событий не выполнен,
следовательно, график содержит контур
и расчет наиболее поздних сроков
наступления событий также не может быть
выполнен.}
else
begin
L[Num[N]]:=E[Num[N]];
for i:=N-1 downto 1 do
begin
L[Num[i]]:=maxValue;
for j:=1 to N do
if L[Num[j]]-T[Num[i],Num[j]]<L[Num[i]] then
L[Num[i]]=E[Num[j]]-T[Num[i],Num[j]]
end;
RaschetEL:=true
end
end;
var i:integer;
Begin {Главная программа}
Здесь необходимо организовать ввод сетевого графика, т.е. ввод матрицы
T размера N на N.
if RaschetEL(T,N,Num,E,L) then
Здесь можно вывести информацию о новых номерах вершин (массив Num),
информацию о наиболее ранних (массив E) и наиболее поздних (массив L) сроках
наступления событий.
Также можно выдать информацию о критических операциях, критическом пути
и рассчитать резервы времени.
else
writeln('Сетевой график задан неверно (содержит контур)')
End.
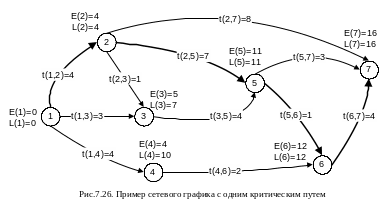
Пример расчета наиболее ранних и наиболее поздних сроков наступления событий представлен на рис.7.24. Расчет состоит из следующих этапов:
E(1)=0;
E(2)=E(1)+t(1,2)=0+4=4;
E(3)=max{E(1)+t(1,3), E(2)+t(2,3)}=max{4+1, 0+3}=5;
E(4)=E(1)+t(1,4)=0+4=4;
E(5)=max{E(2)+t(2,5), E(3)+t(3,5)}=max{4+7, 5+4}=11;
E(6)=max{E(4)+t(4,6), E(5)+t(5,6)}=max{4+2, 11+1}=12;
E(7)=max{E(2)+t(2,7), E(5)+t(5,7), E(6)+t(6,7)}=max{4+8, 11+3, 12+4}=16;
L(7)=E(7)=16;
L(6)=L(7)-t(6,7)=16-4=12;
L(5)=min{L(7)-t(5,7), L(6)-t(5,6)}=min{16-3, 12-1}=11;
L(4)=L(6)-t(4,6)=12-2=10;
L(3)=L(5)-t(3,5)=11-4=7;
L(2)=min{L(7)-t(2,7), L(5)-t(2,5), L(3)-t(2,3)}=min{16-8, 11-7, 7-1}=4;
L(1)=min{L(4)-t(1,4), L(3)-t(1,3), L(2)-t(1,2)}=min{10-4, 7-3, 4-4}=0.
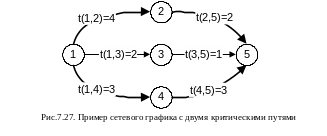
Операция (x,y), для которой E(x)=L(x) и E(y)=L(y) является критической и задержка ее выполнения приведет к задержке выполнения всего проекта. На рис.7.26 дуги, соответствующие критическим операциям выделены жирно. Такие дуги образуют путь из начального события в конечное событие. Этот путь называется критическим. В данном случае такой путь один, хотя в общем случае сетевой график может содержать много критических путей. Простейший пример сетевого графика содержащего два критических пути представлен на рис.7.27.
