7.1.1.Поиск элемента в неупорядоченном массиве
Работа алгоритма поиска элемента в неупорядоченном массиве заключается в том, что элементы массива, начиная с первого, последовательно сравнивается с искомым элементом. Сравнение элементов продолжается до тех пор, пока не будут просмотрены все элементы или очередной элемент массива не равен искомому. Такой поиск называется линейным поиском.
Один из вариантов реализации процедуры поиска элемента в неупорядоченном массиве был рассмотрен в разд.2.4.4 (см. рис.2.13 и листинг 2.4, функция LOCATE). Реализация алгоритма поиска содержат проверку на окончание массива и проверку на равенство текущего элемента массива с искомым. Обе проверки осуществляется для каждого очередного элемента массива. Поэтому в том случае, когда искомого элемента в массиве нет, будет произведено 2n проверок, где n число элементов массива. Однако число проверок можно уменьшить, если в конец массива включить (n+1)-й элемент, равный искомому. Тогда проверка на окончание массива становится лишней. Остается лишь проверка на совпадение очередного элемента с искомым. Если этот элемент находится внутри массива, то поиск заканчивается удачно и элемент считается найденным. Если же этот элемент оказался (n+1)-ым, то искомого элемента в массиве нет. Подобный прием позволяет упростить условия выхода из цикла и используется в программировании довольно часто. Применив этот прием, получим модифицированный алгоритм оператора LOCATE. Данный алгоритм представлен блок-схемой на рис. 7.1. Реализация функции LOCATE представлена в листинге 7.1.
Листинг 7.1
function LOCATE(x:elementtype; L:LIST):position;
var
q:position;
begin
L.elements[L.last+1]:=x;
q:=1;
while L.elements[q]<>x do q:=q+1;
return(q) {Если элемент x не найден, то возвращается позиция L.last+1}
end; {LOCATE}
7.1.2.Поиск элемента в упорядоченном массиве.
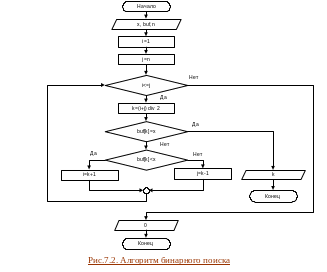
Поиск элемента в упорядоченном массиве может быть осуществлен с помощью алгоритма бинарного поиска. Принцип, лежащий в основе алгоритма бинарного поиска (и некоторых других алгоритмов), состоит в том, что иногда удаётся последовательно уменьшать объём задачи до такой степени, что её решение, в конце концов, становится тривиальным. Главный шаг при бинарном поиске – взять элемент из середины массива и, если он не равен искомому, то в зависимости от его значения исключить из рассмотрения ту или другую половину массива. Повторное выполнение этого шага быстро сокращает размер области поиска.
Алгоритм бинарного поиска для массива, упорядоченного по возрастанию.
1.Определить середину массива.
2.Если элемент, находящийся в середине массива, совпадает с искомым, то поиск завершен.
3.Если элемент, находящийся в середине массива, больше искомого, применить бинарный поиск к первой половине массива.
4.Если элемент, находящийся в середине массива, меньше искомого, бинарный поиск необходимо применить ко второй половине массива.
5. Пункт 1-4 повторять, пока размер области поиска не уменьшается до нуля. Если это произойдет – ключа в массиве нет.
Алгоритм бинарного поиска для массива, упорядоченного по убыванию, реализуйте самостоятельно.
Рассмотренный алгоритм бинарного поиска представлен блок-схемой на рис.7.2. Реализация алгоритма представлена в листинге 7.2.
Листинг 7.2
function BinFind(x:elementtype; n:position; buf:arraytype):position;
{ Функция BinFind осуществляет бинарный поиск элемента x в массиве buf длины n.
Возвращает номер элемента x в массиве buf, если элемент найден,
и 0, в противном случае.}
var i,j,k:position;
begin
i:=1; j:=n;
while i<=j do
begin
k:=(i+j) div 2;
if buf[k]=x then return(k);
if buf[k]<x then i:=k+1
else j:=k-1;
end;
return (0)
end;
Нетрудно заметить, что в худшем случае (искомого элемента в массиве нет) алгоритм бинарного поиска сделает не более O(log2N) шагов. Это объясняется тем, что на каждом шаге поиска вдвое уменьшается область поиска. До того, как она станет равной одному элементу, произойдет не более O(log2N) таких уменьшений.