2.4.4.Реализация списков
В этом разделе речь пойдет о нескольких структурах данных, которые можно использовать для представления списков. Мы рассмотрим реализации списков с помощью массивов, указателей и курсоров. Каждая их этих реализаций осуществляет определенные операторы, выполняемые над списками, более эффективно, чем другая.
Реализация списков посредством массивов
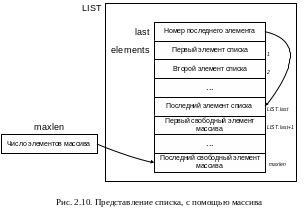
При реализации списков с помощью массивов элементы списка располагаются в смежных ячейках массива. На рис 2.10 представлена одна из возможных реализаций. В данном случае список представлен записью LIST, состоящей из поля last, указывающей на последний элемент списка и массива elements, в котором располагаются элементы списка. Поскольку элементы массива elements нумеруются с единицы, то значение last равно числу элементов списка. Длина массива elements храниться в константе maxlen.
Такое представление списка позволяет легко просматривать содержимое списка и вставлять новые элементы в его конец. Но вставка нового элемента в середину списка требует перемещения всех последующих элементов на одну позицию к концу массива, чтобы освободить место для нового элемента. Удаление элемента также требует перемещения элементов, чтобы закрыть освободившуюся ячейку.
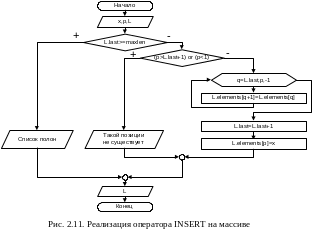
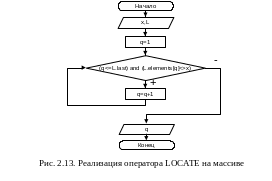
Алгоритмы операторов INSERT, DELETE и LOCATE списка, реализованного на массиве, представлены блок-схемами на рис. 2.11, 2.12 и 2.13 соответственно.
Реализация рассмотренной СД и операторов INSERT, DELETE и LOCATE на языке Pascal представлена в листинге 2.4.
Реализацию остальных операторов списка сделайте самостоятельно.
Листинг 2.4
const
maxlen=100; { или другое подходящее число }
type
elementtype=real; { тип элементов списка}
position=integer;
LIST = record
elements:array[1..maxlen] of elementtype;
last:position
end;
function END(L:LIST):position;
begin
return(L.last+1)
end; { END }
function LAST(L:LIST):position;
begin
return(L.last)
end; { LAST }
procedure INSERT(x:elementtype; p:position; var L:LIST);
(INSERT вставляет элемент x в позицию p в списке L}
var
q:position;
begin
if L.last>=maxlen then
error('Список полон')
else if (p>L.last+1) or (p<1) then
error('Такой позиции не существует')
else
begin
for q:=L.last downto p do {Перемещение элементов из позиций p, p+1, ... на
одну позицию к концу списка }
L.elements[q+1]:=L.elements[q];
L.last:=L.last+1;
L.elements[p]:=x
end
end; {INSERT}
procedure DELETE(p:position; var L:LIST);
{DELETE удаляет элемент в позиции p списка L}
var
q:position;
begin
if (p>L.last) or (p<1) then
error('Такой позиции не существует')
else
begin
L.last:=L.last-1;
for q:=p to L.last do {Перемещение элементов из позиций p+1,p+2,... на
одну позицию к началу списка }
L.elements[q]:=L.elements[q+1];
end
end; {DELETE}
function LOCATE(x:elementtype; L:LIST):position;
{LOCATE возвращает позицию элемента x в списке L}
var
q:position;
begin
q:=1;
while (q<=L.last)and(L.elements[q]<>x) do
q:=q+1;
return(q);
end; {LOCATE}