2.4.Методы организации данных в памяти эвм

2.4.1.Типы данных, структуры данных и абстрактные типы данных

Термины тип данных (или просто тип) переменной обозначает множество значений, которые может принимать эта переменная. Набор базовых типов данных отличается в различных языках.

Абстрактный тип данных (АТД) — это математическая модель плюс различные операторы, определенные в рамках этой модели. Как уже указывалось, мы можем разрабатывать алгоритм в терминах АТД, но для реализации алгоритма в конкретном языке программирования необходимо найти способ представления АТД в терминах типов данных и операторов, поддерживаемых данным языком программирования.

Для представления АТД используются структуры данных, которые представляют собой набор переменных, возможно, различных типов данных, объединенных определенным образом.

Базовым строительным блоком структуры данных является ячейка, которая предназначена для хранения значения определенного базового или составного типа данных. Структуры данных создаются путем задания имен совокупностям (агрегатам) ячеек и (необязательно) интерпретации значения некоторых ячеек как представителей (указателей) других ячеек.

В качестве простейшего механизма агрегирования ячеек в большинстве языков программирования можно применять (одномерный) массив, т.е. последовательность ячеек определенного типа. Массив также можно рассматривать как отображение множества индексов в множество ячеек.

Другим общим механизмом агрегирования ячеек в языках программирования является структура (запись). Запись можно рассматривать как ячейку, состоящую из нескольких других ячеек (называемых полями), значения в которых могут быть разных типов. Записи часто группируются в массивы; тип данных определяется совокупностью типов полей записи.

Массивы и записи являются структурами с произвольным доступом, подразумевая под этим, что время доступа к компонентам массива или записи не зависит от значения индекса массива или указателя поля записи.

Третий метод агрегирования ячеек, который можно найти в языках программирования это файл. Файл, как и одномерный массив, является последовательностью значений определенного типа. Различают файлы прямого и последовательного доступа. В файле прямого доступа имеет индекс, т.е. все ячейки (компоненты) файла пронумерованы. Доступ может быть осуществлен к любой ячейки. Файл последовательного доступа не имеет индексов: его элементы доступны только в том порядке, в каком они были записаны в файл.

Достоинство агрегирования с помощью файла заключается в том, что файл не имеет ограничения на количество составляющих его элементов и это количество может изменяться во время выполнения программы.

В дополнение к средствам агрегирования ячеек в языках программирования можно использовать указатели и курсоры. Указатель — это ячейка, чье значение указывает на другую ячейку. При графическом представлении структуры данных в виде схемы тот факт, что ячейка А является указателем на ячейку В, показывается с помощью стрелки от ячейки А к ячейке В.

Курсор — это ячейка с целочисленным значением, используемая для указания на массив. В качестве способа указания курсор работает так же, как и указатель, но курсор можно использовать и в языках, которые не имеют явного типа указателя.

В схемах структур данных принято рисовать стрелку из ячейки курсора к ячейке, на которую указывает курсор. Иногда также указывают целое число в ячейке курсора, напоминая тем самым, что это не настоящий указатель.

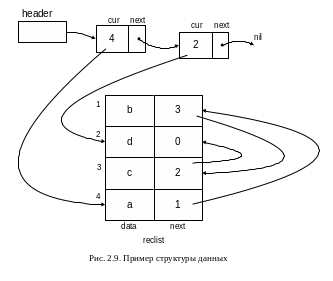
Пример структуры данных представлен на рис.2.9. В данной структуре ячейка header содержит указатель на запись, состоящую из двух полей: cur и next. Поле cur содержит курсор, содержащий индекс логически первого элемента массива reclist (в данном случае четвертый элемент массива является логически первым, см. ниже). Поле next содержит указатель на аналогичную запись, в которой поле cur содержит курсор на логически последнюю запись массива reclist (в примере это вторая запись), а поле next содержит пустой указатель. Массив reclist состоит из четырех записей с индексами от 1 до 4. Каждая запись состоит из двух полей: data и next. Поле data содержит данные (в примере это символы a,b,c,d). Логический порядок элементов массива определяется значением курсора в поле next - курсор хранит индекс логически следующего элемента массива. Так за четвертым элементом следует первый, за первым - третий, за третьим - второй. Второй элемент массива логически последний, т.к. значение поля next второго элемента равно 0, т.е. отличается от любого значения индекса массива - 1,2,3 или 4.