Монотонная функция, сложная и обратная функции.
def:
Функцыю
называюць нарастальнай
на
мностве
,
калі
;
неспадальнай,
калі
;
спадальнай,
калі
;
ненарастальнай,
калі
.
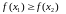Усе такія функцыі называюцца манатоннымі.
Нарастальныя і спадальныя функцыі
называюцца строга
манатоннымі.
def:
Няхай функцыя
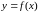вызначаная на
і строга манатонная на
,
г.зн.
,
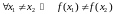а тым самым
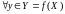існуе толькі адзін лік
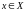такі, што
.
Такім чынам на мностве
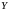вызначана функцыя, якая называецца
адваротнаю
функцыяй
да функцыі
і абазначаецца
.
Відочна, што
,
а
def:
Няхай функцыя
вызначана
на
,
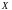а функцыя
вызначана на
,
прычым
.
Тады функцыю, якая
набывае значэнне
,
называюць складанай
функцыяй (або
кампазіцыяй,
або суперпазіцыяй)
функцый
і абазначаюць
.
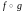Эквивалентные функции. Бесконечно малые функции более высокого порядка.
def:
Калі
і
,
то кажуць, што функцыя
у акрузе пункта
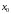ёсць
бясконца малая больш высокага парадку,
чым
.
У
сувязі з уведзеным абазначэннем часта
выкарыстоўваецца запіс
.
Гэта азначае
–
бясконца малая ў пункце
.
def:
Калі функцыі
і
вызначаны ў праколатай акрузе пункта
і
,
то функцыі
называюць эквівалентнымі
ў акрузе пункта
і пішуць
.
Производная функции, односторонние производные.
def.
Няхай функцыя
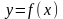вызначана ў акрузе пункта
.
Калі існуе
,
то гэты ліміт называецца вытворнай
функцыі
у пункце
.
def.
Калі існуюць
і
то іх называюць адпаведна левабаковай
і
правабаковай вытворнымі функцыі
у пункце
і
абазначаюць адпаведна
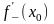і
.
З
уласцівасцяў лімітаў вынікае: функцыя
мае вытворную ў пункце
,
калі і толькі калі яна мае левабаковую
і правабаковую вытворныя:
=
,прычым
=
=
.
20.
Геометрический
смысл производной
вытворная
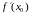функцыі
пункце
ёсць вуглавы каэфіцыент датычнай да
графіка функцыі ў пункце
.
Дифференциал. Инвариантность формы дифференциала
def.
Галоўную лінейную частку
прыросту дыферанцавальнай ў пункце
функцыі
(гл. (1)) называюць дыферэнцыялам
функцыі і абазначаюць
.
Такім
чынам,
Тэарэма 2
(інварыянтавасць формы дыферэнцыяла).
Дыферэнцыял функцыі
мае адзін і той самы выгляд
не гледзячы на тое, ці ёсць x
незалежная зменная, ці х – дыферэнцавальная
функцыя якой-небудзь іншай зменнай.
□ Няхай
ёсць дыферэнцавальная функцыя зменнай
t
. Тады складаная
функцыя
мае вытворную
,
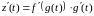а
таму
.
■
Локальный экстремум функции.
def.
Няхай існуе
–акруга
пункта
,
,
ў якой вызначана функцыя
і
.
Тады кажуць, што функцыя
мае ў пункце
лакальны
максімум (мінімум).
Лакальны максімум і лакальны мінімум
аб’ядноўваюць агульным тэрмінам
лакальны
экстрэмум.
Первообразная и неопределённый интеграл.
def.
Дыферэнцавальная на інтэрвале Х
функцыя
называецца першаіснаю
для функцыі
на
Х, калі
def.
Калі
ёсць першаісная для
на інтэрвале Х
, то сукупнасць
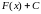першаісных для
называюць
нявызначаным інтэгралам ад функцыі
на
Х
і абазначаюць
.
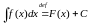Интегральная сумма и определённый интеграл для функции
на отрезке
.
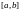Няхай
функцыя
вызначана на адрэзку
(магчыма разрыўная, магчыма непарыўная,
магчыма недыферэнцавальная, магчыма
дыферэнцавальная ў пунктах адрэзка).
Няхай
– сукупнасць пунктаў гэтага адрэзка
такіх, што
.
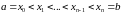Мноства гэтых пунктаў назавем падзелам
адрэзка
і абазначым
.
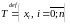Адрэзкі
назавем адрэзкамі
падзелу
,
або частковымі
адрэзкамі
адрэзка
.
Абазначым
праз
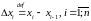даўжыні адрэзкаў
.
Лік
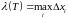назавем дробнасцю
падзелу
.
Мноства пунктаў
будзем называць выбаркай
з
адрэзка
.
Суму
будзем называць інтэгральнаю
сумай для
функцыі
пры зададзеным падзеле
і фіксаванай выбарцы
.
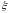def.
Лік I
называюць вызначаным
інтэгралам
функцыі
на адрэзку
і абазначаюць
, калі
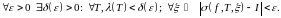(1)
Пры
гэтым таксама кажуць, што існуе
ліміт
інтэгральных сумаў
пры
,
і гэты ліміт не залежыць ні ад падзелу
,
ні ад выбаркі
і пішуць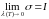
Верхняя и нижняя суммы Дарбу
Сумы
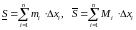называюцца
адпаведна ніжняй
і верхняйсумамі
Дарбу
для дадзенага падзелу
.
Монотонность и аддитивность определённого интеграла.
(манатоннасць
інтэграла). Калі
функцыі
і
інтэгравальныя на
і
, то
.
(адытыўнасць інтэграла) Калі функцыя інтэгравальная на , то
.
Интеграл с переменной верхней границей.
Калі
функцыя
ёсць інтэгравальная на
,
то
існуе інтэграл
,
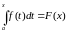(1)
які называюць інтэгралам са зменнаю верхняю мяжою.
Несобственный интеграл по бесконечному промежутку (НИ-1).
def.
Ліміт
называюць
неўласцівым інтэгралам ад функцыі
на бясконцым прамежку
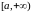, або неўласцівым
інтэгралам першага роду
(НІ-1) і абазначаюць
.
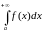
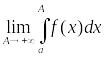Абсолютная и условная сходимость НИ-1.
def.
Калі інтэграл
ёсць збежны, а
– разбежны, то інтэграл
называецца ўмоўна
збежным.
def. Неўласцівы інтэграл называецца абсалютна збежным, калі інтэграл ёсць збежны.
Особая точка функции.Несобственный интеграл от неограниченной функции (НИ-2)
def.
Калі функцыя
ёсць неабмежаваная ў пункце
,
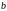і інтэгравальная на кожным адрэзку
( упрыватнасці
ёсць абмежаваная на адрэзку
),
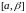то пункт
называюць асаблівым
пунктам
функцыі
.
def. Ліміт
(1)
называюць неўласцівым інтэгралам ад неабмежаванай функцыі на адрэзку (або неўласцівым інтэгралам другога роду, НІ-2) і абазначаюць
.
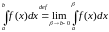(2)
Калі існуе канечны ліміт (1), то Ні-2 (2) называюць збежным. Калі ж ліміт (1) не існуе, то кажуць, што інтэграл (2) ёсць разбежны.