
- •Точные верхняя и нижняя границы множества. Записать при помощи математических символов.
- •Кратный корень многочлена.
- •Неограниченная и бесконечно большая числовая последовательность.
- •Бесконечно малая, сходящаяся, расходящаяся числовая последовательность.
- •Числовой ряд.Сходимость числового ряда
- •Монотонная числовая последовательность.
- •Последовательности вложенных и стягивающихся отрезков.
- •Подпоследовательность числовой последовательности. Частичный предел.
- •Фундаментальная числовая последовательность.
- •Предел функции в точке и на , бесконечный предел. Односторонние пределы
- •Непрерывность функции в точке и на множестве.
- •Первая и вторая тэоремы Вейерштрасса..
- •Равномерная непрерывность.
- •Точка разрыва функции. Типы разрывов.
- •Монотонная функция, сложная и обратная функции.
- •Эквивалентные функции. Бесконечно малые функции более высокого порядка.
- •Производная функции, односторонние производные.
Ограниченное множество. Верхняя и нижняя границы множества.
def:
Мноства
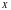 называецца абмежаваным
зверху [знізу],
калі
называецца абмежаваным
зверху [знізу],
калі
 вещественное число
вещественное число
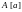 такі, што
такі, што
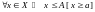 .
Лікі
.
Лікі
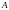 і
і
 называюць адпаведна верхняй
і
ніжняй
межамі мноства
.
Мноства, абмежаванае як зверху, так і
знізу называецца абмежаваным.
называюць адпаведна верхняй
і
ніжняй
межамі мноства
.
Мноства, абмежаванае як зверху, так і
знізу называецца абмежаваным.
Точные верхняя и нижняя границы множества. Записать при помощи математических символов.
def:
Найбольшая з ніжніх межаў абмежаванага
знізу мноства
называецца яго дакладнай
ніжняй мяжою
і абазначаецца
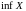 (чытаецца: інфімум).
(чытаецца: інфімум).
def:
Найменшая з верхніх межаў абмежаванага
зверху мноства
называецца яго дакладнай
верхняй мяжою
і абазначаецца
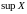 (чытаецца: супрэмум).
(чытаецца: супрэмум).
Зразумела, што згаданыя азначэнні верхняй і ніжняй межаў можна наступным чынам запісаць пры дапамозе матэматычных сымбаляў:
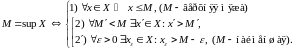
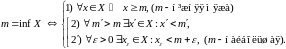
Неограниченность множества сверху и снизу. (
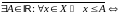
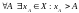 ,
[
,
[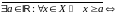
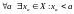 ]
]Кратный корень многочлена.
def:
Лік
 называецца коранем
мнагаскладу
называецца коранем
мнагаскладу
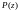 кратнасці
кратнасці
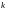 ,
калі мае месца выяўленне
,
калі мае месца выяўленне
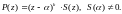
Неограниченная и бесконечно большая числовая последовательность.
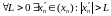
def:
Лікавая паслядоўнасць
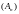 называецца бясконца
вялікаю паслядоўнасцю
(бвп),
калі
называецца бясконца
вялікаю паслядоўнасцю
(бвп),
калі
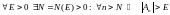 .
Гэтае азначэнне раўназначнае таму, што
ў (бвп)
толькі канечная колькасць элементаў
належыць адрэзку
.
Гэтае азначэнне раўназначнае таму, што
ў (бвп)
толькі канечная колькасць элементаў
належыць адрэзку
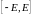 .
.
Бесконечно малая, сходящаяся, расходящаяся числовая последовательность.
def:
Лікавая паслядоўнасць
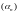 называецца бясконца
малою паслядоўнасцю (бмп),
калі
называецца бясконца
малою паслядоўнасцю (бмп),
калі
 .
Гэтае азначэнне раўназначнае таму, што
ў (бмп)
толькі канечная колькасць элементаў
належыць мноству
.
Гэтае азначэнне раўназначнае таму, што
ў (бмп)
толькі канечная колькасць элементаў
належыць мноству
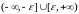 ,
або знаходзіцца па-за інтэрвалам
,
або знаходзіцца па-за інтэрвалам
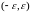 .
.
def:
Лікавая паслядоўнасць
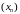 называецца збежнай
, калі існуе такі лік
называецца збежнай
, калі існуе такі лік
 ,
што паслядоўнасць
,
што паслядоўнасць
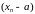 ёсць (бмп),
што раўназначна запісу
ёсць (бмп),
што раўназначна запісу
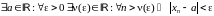 .
Пры гэтым пішуць
.
Пры гэтым пішуць
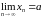 , або
, або
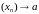 і кажуць, што паслядоўнасць
мае ліміт
.
Калі такі лік
не існуе, то лікавая паслядоўнасць
называецца разбежнаю.
і кажуць, што паслядоўнасць
мае ліміт
.
Калі такі лік
не існуе, то лікавая паслядоўнасць
называецца разбежнаю.
Заўвага 1. Бясконца малая паслядоўнасць ёсць збежная паслядоўнасць, а яе ліміт роўны нулю.
Числовой ряд.Сходимость числового ряда
def:
Няхай
–лікавая
паслядоўнасць. Выраз выгляду
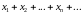 ,
або
,
або
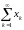
называецца
лікавым
шэрагам,
а
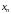 –яго
–яго
 –ым
складнікам.
Лік
–ым
складнікам.
Лік
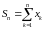 называецца
-й
частковай сумай
шэрагу (1). Шэраг (1) называецца збежным
, калі паслядоўнасць яго частковых сумаў
называецца
-й
частковай сумай
шэрагу (1). Шэраг (1) называецца збежным
, калі паслядоўнасць яго частковых сумаў
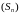 ёсць збежная. Калі паслядоўнасць
мае ліміт
ёсць збежная. Калі паслядоўнасць
мае ліміт
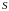 ,
то лік
называюць сумай
шэрагу
(1) і пішуць
,
то лік
называюць сумай
шэрагу
(1) і пішуць
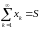 .
Калі паслядоўнасць
ёсць разбежная, то кажуць, што шэраг (1)
– разбежны.
.
Калі паслядоўнасць
ёсць разбежная, то кажуць, што шэраг (1)
– разбежны.
Монотонная числовая последовательность.
def:
Лікавая паслядоўнасць
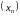 называецца нарастальнай,
калі
называецца нарастальнай,
калі
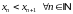 ;
неспадальнай,
калі
;
неспадальнай,
калі
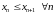 ;
спадальнай,
калі
;
спадальнай,
калі
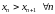 ;
ненарастальнай,
калі
;
ненарастальнай,
калі
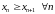 .
(Пры гэтым будзем іх абазначаць адпаведна
.
(Пры гэтым будзем іх абазначаць адпаведна
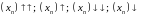 .)
Усе такія лікавыя паслядоўнасці
называюцца манатоннымі
(абазначаюцца
.)
Усе такія лікавыя паслядоўнасці
называюцца манатоннымі
(абазначаюцца
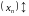 ).
Нарастальныя і спадальныя паслядоўнасці
называюцца строга
манатоннымі (абазначаюцца
).
Нарастальныя і спадальныя паслядоўнасці
называюцца строга
манатоннымі (абазначаюцца
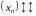 ).
).
Последовательности вложенных и стягивающихся отрезков.
def:
Паслядоўнасць адрэзкаў лікавай прамой
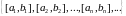 такіх, што
такіх, што
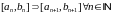 называецца паслядоўнасцю
ўкладзеных адрэзкаў.
Пры гэтым праўдзяцца няроўнасці
называецца паслядоўнасцю
ўкладзеных адрэзкаў.
Пры гэтым праўдзяцца няроўнасці
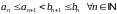 .
.
def:
Калі выконваецца роўнасць
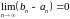 ,
то
паслядоўнасць укладзеных адрэзкаў
называецца паслядоўнасцю
сцягвальных адрэзкаў.
,
то
паслядоўнасць укладзеных адрэзкаў
называецца паслядоўнасцю
сцягвальных адрэзкаў.
Подпоследовательность числовой последовательности. Частичный предел.
def:
Няхай
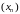 ёсць некаторая лікавая паслядоўнасць,
а
ёсць некаторая лікавая паслядоўнасць,
а
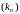 адвольная нарастальная паслядоўнасць
натуральных лікаў, г.зн.
адвольная нарастальная паслядоўнасць
натуральных лікаў, г.зн.
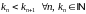 ,
прычым
,
прычым
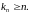 Паслядоўнасць
Паслядоўнасць
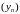 ,
агульны элемент якой
,
агульны элемент якой
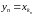 ,
г.зн. паслядоўнасць
,
г.зн. паслядоўнасць
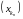 называюць падпаслядоўнасцю
лікавай
паслядоўнасці
.
Такім чынам, калі з паслядоўнасці
выбраць элементы з нумарамі
называюць падпаслядоўнасцю
лікавай
паслядоўнасці
.
Такім чынам, калі з паслядоўнасці
выбраць элементы з нумарамі
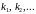 ,
то атрымаецца падпаслядоўнасць
,
то атрымаецца падпаслядоўнасць
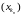 .
Калі падпаслядоўнасць
збежная, то яе ліміт называецца частковым
лімітам паслядоўнасці
.
.
Калі падпаслядоўнасць
збежная, то яе ліміт называецца частковым
лімітам паслядоўнасці
.
