20)Основные понятия метода сеток для приближенного решения уравнений математической физики. Основные этапы, виды сеток и шаблоны для конечно-разностной аппроксимации производных. Погрешности метода.

Для решения задач с диф уравнениями в частных производных наибольшее распространение нашел метод конечных разностей. В данном применении он называется метод сеток и сводит решение уравнений в частных производных и и систем к решению систем линейных, как правило, алгебраических уравнений с достаточно разряженными матрицами коэффициентов.

Построение решения в методе сеток осуществляется в 3 этапа:

1 Построение в области решения сетки из узловых точек. Конфигурация сетки должна соответствовать характеру задачи и граничным условиям, т.е. вид сетки определяется формой области решения.

Виды сеток:

А) прямоугольная б) полярная в)треугольная г)скошенная

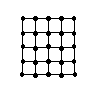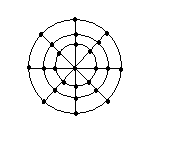а б в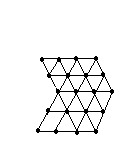

г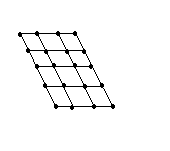

2 Конечно-разностная аппроксимация производных искомой функции, входящих в уравнения задачи. С этой целью выбирают вычислительный шаблон разностной схемы – набор(конфигурацию) узлов, с помощью которых производится замена производных конечными разностями. Шаблон , содержащий p точек, называется p-точечным. Например, для аппроксимации производных второго порядка, входящих в оператор Лапласа , применяют пятиточечный шаблон, показанный на рисунке1

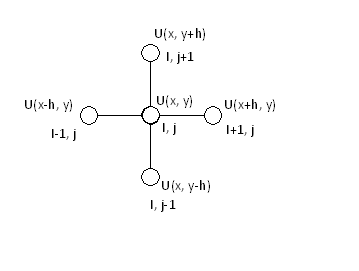
В соответствии с выбранным шаблоном получают выражения для аппроксимации частных производных

Введем для сокращения записи общепринятые индексные обозначения узлов в соответствии с рис.1 и соответствующие обозначения сеточных функций в узлах и т д . тогда выражения для производных принимают вид :

Полученные конечно-разностные аппроксимации имеют второй порядок точности.

Разностные аппроксимации производных подставляют в уравнения задачи и получают систему алгебраических сеточных уравнений, связывающих значения сеточной функции в соседних узлах.

3 Решение полученной системы алгебр уравнений подходящим методом с целью получения приближенного решения в узлах сетки. При этом число уравнений системы равно числу узлов разностной сетки. Число уравнений может быть весьма велико, т.к. с увеличением числа узлов уменьшается погрешность аппроксимации производных. (может достигать нескольких сотен или даже тысяч).

В каждое сеточное уравнение входит небольшое количество соседних неизвестных(5 при пятиточесном шаблоне), хотя вся система содержит порядка неизвестных. Таким образом, матрица системы является сильно разряженной. Прямые методы решения таких систем (если сеточные уравнения -линейные) неэффективны. Поэтому системы с такими матрицами решают с помощью итерационных методов : простой итерации, Зейделя, релаксационных. Решение системы при использовании таких методов получают с заданной погрешностью.

21.Решение задачи Дирихле для уравнения Лапласа

При решении эллиптических уравнений в частных производных часто ставится задача Дирихле (первая краевая задача): отыскание решения в неко­торой области пространства при заданных значениях искомой функции на границе области. Иллюстрацией задачи Дирихле является задача нахождения решения уравнения Лапласа

x,yϵG (1)

с заданным граничным условием

u(x;y)│_Г=φ(x;y) (2)

Здесь Г - граница области G, в которой ищется решение и(х, у), удовлетво­ряющее уравнению (1) и граничному условию (2).

Такая постановка задачи имеет место, например, при расчете стационар­ных тепловых полей в физике, а также при определении деформаций в строи­тельной механике.

Д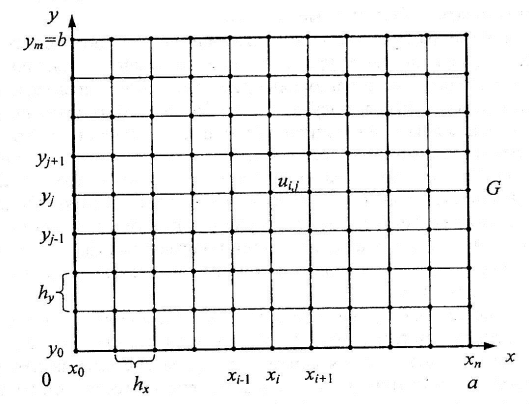 ля упрощения примем, что область решения G имеет прямоугольную форму G = {(x,y)│0<x<a,0<y<b} , как показано на рис. 5.4.

Рис. 5.4. Область решения задачи Дирихле

Тогда граничное условие (2) можно представить в следующем виде: и(0,y) = f₁(y), и(а,у) = f2(у), уϵ[0,b]

u(x,0) = f₃(x), u(x,b) = f₄(x), хϵ[0,a],

f₁ (y), f₂ (y) , f₃ (х), f₄ (х) - заданные функции.

и(х,у) непрерывна на границе области G, т.е. f₁(0) = fз(0),

f₂ (b)=f₄(0), f₂ (0) = f_З(а), f₂(Ь) = f₄(а).

Для получения решения поставленной задачи используем метод сеток.

Нa первом этапе метода в области решения G строим равномерную сетку из узловых точек (см. рис. 5.4). Количество точек по направлениям х и у обо­значим, соответственно, n и т. Для упрощения выкладок примем, что шаги разностной сетки по направлениям хну одинаковы, т. е. h_x = h_y = h (квад­ратная сетка). Обозначим координаты узловых точек

x_i=i*h, i = 0,1,...,n; y_j = j*h, j = 0,1,...,m

где i, j - номера точек по направлениям хи у, соответственно.

Искомую функцию в узловых точках обозначим, как u_i;j= u{x_i;y_j).

На втором этапе в каждом внутреннем узле сетки аппроксимируем част­ные производные, входящие в уравнение Лапласа, центральными конечно-разностными отношениями:

Получим систему сеточных уравнений вида

(3)

На третьем этапе нужно решить систему сеточных уравнений (3) с целью получения значений и_i;j во всех внутренних узлах сетки. В силу ли­нейности уравнения Лапласа, система уравнений (3) является системой линейных алгебраических уравнений с сильно разряженной матрицей коэф­фициентов (в каждое уравнение входит только пять неизвестных). Такая сис­тема наиболее эффективно решается итерационными методами.(м-д Зейделя).