17. Метод самогонки

Метод прогонки представляет собой модификацию метода исключения Гаусса для системы с 3-диагональной матрицей коэффициентов. Алгоритм метода включает прямой и обратный ходы. На прямом ходе (вниз по системе) вычисляются прогоночные коэффициенты.

Прямой ход начинается с определения начальных прогоночных коэффициентов: и затем по рекуррентным соотношениям вычисляют прогоночные коэффициенты .

На обратном ходе (вверх по системе) через прогоночные коэффициенты вычисляются искомые неизвестные системы. Сначала вычисляются: , а затем остальные неизвестные по рекуррентным формуле:

Устойчивость и корректность метода прогонки обеспечивается условием преобладания диагональных коэффициентов в 3-диагональной системе:

С хема алгоритма

y_n=d₂u_n-1 + dh/d₁h+d₂(1-v_n-1)

h=b-a/n

v₀=-c₂/c₁*h – c₂

u₀=-ch/c₁h-c₂

x=a+ih

α=1-p(x)*h/2

β=q(x)*h²-2

=1+p(x)*h/2

=f(x)*h²

V_i=- /β+αv_i-1

u_i= – αv_n-1/ β+αv_i-1

y_i=u_i+v_iy_i+1

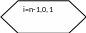
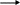
18)Основные понятия и классификация дифференциальных уравнений в частных производных (уравнения математической физики)

В общем случае дифф уравнением в частных производных называют уравнение, связывающее между собой независимые переменные, а также искомую функцию и её частные производные.[ИЛИ уравнение,в котором искомая величина зависит от нескольких других величин]

Общий вид:

F(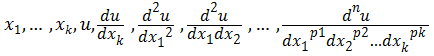 ) = f( ) (1)

Здесь + . . . + =n

Наивысший порядок входящей в диф уравнение производной n называется порядком диф уравнения.

Если f( ) = 0,то уравнение называется однородным, в противном случае- неоднородным.

Если функция линейна относительно функции и ее производные, то уравнение (1) называется линейным уравнением в частных производных..

Диф уравнение называется квазилинейным, если функция линейна по высшим производным(n-ого порядка),иными словами, коэффициенты при высших производных зависят лишь от функции и её производных до (n-1) –го порядка.

Решением называется функция u( ) ,имеющая частные производные до требуемого порядка и обращающая уравнение (1) в тождество.

В классических уравнениях математической физики в качестве независимых переменных присутствуют время и пространственные координаты.

Задача называется стационарной, если решение не зависит от времени, и нестационарной или эволюционной, если оно зависит от времени.

Задачи с одной пространственной переменной называются одномерными, с двумя - двумерными и т д.

Диф уравнения в частных производных классифицируют либо в зависимости от их математической природы, либо в зависимости от физического смысла решаемых с их помощью задач

В канонической форме:

+ B(x,y) + F(x,y,u, ) = 0 (2)

Где А, В, С – коэффициенты функции

Дополнительными условиями могут служить граничные условия(краевая задача) или начальные условия (задача Коши), а также комбинация тех и других (смешанная краевая задача).

Математическая классификация в зависимости от характера функций А, В и С.

Обозначим D = – АС ,тогда

При D=0 уравнение (2) называется параболическим,

При D>0 –гиперболическим

При D<0 – эллиптическим.

Тип одного и того же уравнения может меняться в зависимости от области пространства.

Эллиптическое уравнение описывает установившиеся (стационарные) процессы, т.е. задача ставится в замкнутой области и в каждой точке границы этой области задаются граничные условия. Классическим уравнением эллиптич типа является уравнение Лапласа.

Параболическими и гиперболическими уравнениями описываются эволюционные процессы(процессы «распространения»).В таких задачах на одной части границы ставятся граничные условия, на другой – начальные. Примером параболического типа является уравнение теплопроводности, а гиперболического типа – волновое уравнение.