29)Принцип возможных перемещений и построение системы линейных уравнений равновесия для отдельных конечных элементов и для всей системы в целом.

Иначе принцип Лагранжа.

Если тело находится в равновесии и каждой его точке сообщить малое перемещение δU, допускаемое наложенными связями(возможные перемещения), то работа всех сил на возможных перемещениях равна нулю или, по-другому, приращение работы внутренних сил δU равно работе внешних сил δW на возможных перемещениях, т.е. δU= δW.

При этом полная потенциальная энергия П=U-W системы минимальна, т.к. δU- δW=0; δ(U-W)= δП=0.

Работа внутренних сил (потенциальная энергия деформации) в области тела Ω:

, где σ и ε – функции напряжений и деформаций в области Ω.

Работа внешних сил:

W= , где p и u – функции нагрузки и перемещений по области Ω.

Вариационный принцип Лагранжа позволяет получить систему уравнений равновесия исходя из условия минимума функционала полной потенциальной энергии системы. Если считать, что перемещения всех точек тела, uⁱ есть известные функции узловых перемещений qⁱ, то:

(i=1,2,…,n) или

Сравнивая с системой равновесия КЭ, [K]·{q}={R} можно представить

, (i=1,2,..,n), где R_i – узловые нагрузки.

Коэффициент жесткости - это усилие, возникающее по направлению i-той связи от j-го единичного перемещения при условии, что все остальные перемещения равны 0. Из равенства работ внутренних и внешних сил получим

где R_i,j-усилие (реакция) по направлению i-той связи от j-того единичного перемещения (q_j=1).

30. Применение мкэ на примере уравнений равновесия стержня при его сжатии-растяжении

Стержень с 2мя узлами, нагруженный силами N₁ и N₂, работает на растяжение-сжатие.

Ψ – объемный вес стержня

А – площадь сечения

В каждом узле одна степень свободы.

Вектор узловых перемещений КЭ: {q}={u₁,u₂}^T

Вектор узловых сил: {P}={N₁,N₂}^T

Перемещение в произвольной точке с координатой x аппроксимируем линейной функцией

u(x)=α₁+α₂x, где α₁,α₂ – постоянные коэффициенты

В матричной записи: {u}=[1..x]

или {u}=[F] , где [F]=[1..x]-матрица базовой функций, {α}={α₁,α₂}^T- вектор постоянных

Получим выражение для вектора {α}:

{q}= или {q}=[C] , где [C]= – матрица узловых координат.

Отсюда {α}=[C]^-1{q}=

Подставим {α} в {u}: {u}=[F] [C]^-1{q}= =

и тогда {u}=[Ф] , где [Ф] – функции формы или координатные функции.

Найдем выражение для деформаций:

ε_x= или {ε_x}=[A]·[Ф]·{q}, где [A] = .

Обозначим {ε}={ε_x} и [B]=[A]·[Ф]=[A] = тогда {ε}=[B]

Найдем выражение для напряжения:

Из закона Гука σ_x=Eε_x. Имеем {σ}={σ_x}=[D]·{ε} , где [D]=[E], E – модуль упругости материала стержня.

{σ}=[D]·[B]·{q}

Из принципа возможных перемещений получим коэффициенты жесткости и уравнения равновесия стержневого КЭ.

Работа внутренних сил равна работе внешних сил (нагрузки в узлах+сила тяжести).

Подставляем ранее полученные выражения:

, , {σ}=[D]·[B]·{q}

получим:

Это основное матричное уравнение КЭ.

[K]·{q}={R}, где [K]= - матрица жесткости

{R}={P}+ - вектор обобщенных узловых сил (с учетом веса стержня).

Получим матрицу жесткости [K]: (интеграл по объему заменяем интегралом по длине)

, где А – площадь поперечного сечения стержня (величина постоянная).

Тогда [K]=

[B]=

[B]^T = ;

[K]=

Вектор узловых сил {R}=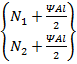

Окончательное уравнение для КЭ:

Решив эту систему, получим узловые перемещение u₁ и u₂, а затем перемещения, деформации и напряжения в любой точке стержня.