27) Основная идея метода конечных элементов (мкэ) для приближенного расчета напряженно-деформированного состояния конструкции.

МКЭ для описания сплошных сред впервые был применен в середине 50-х годов 20-го столетия и с тех пор завоевал известность исключительно полезного инженерного метода. Он широко применяется в различных областях техники. МКЭ – основной численный метод для решения на компе прикладных задач механики сложных конструкций. В строительной механике МКЭ используется для исследования напряженного состояния конструкций сложной геометрической формы. В основе МКЭ лежит универсальный подход, который заключается в представлении геометрии любого деформированного тела в виде совокупности элементов простейшей формы: линейной, треугольной, четырехугольной и др. Примеры конечных элементов:

-одномерные

-плоские

-пространственные

28)Основные этапы мкэ

1)Разделение конструкции на малые элементы простой формы.

Разделение на КЭ можно выполнять разными способами, в зависимости от того, как проще решить задачу.

КЭ плоского тела имеет обычно треугольную или четырехугольную форму, а КЭ трехмерных тел – форму гексаэдров или тетраэдров. Принимают что КЭ взаимодействуют между собой только в заданных узловых точках

2)Выбор схемы интерполяции перемещений внутри элементов.

Схема интерполяции позволяет выразить перемещение любой точки внутри КЭ через его значения в узлах. Обычно перемещение задается простым полиномом(ом-ном-ном) с коэффицентом, определяемым в процессе решения.

3)Определение соотношений между силами и перемещениями в узлах.

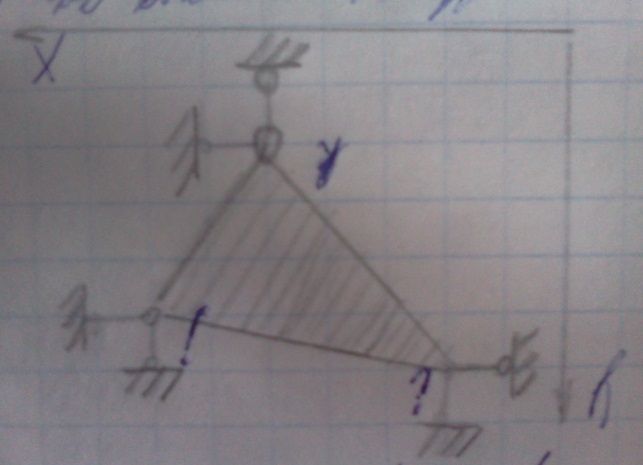
Рассмотрим, как пример, плоский КЭ.

Узлам придаются дополнительные связи. Узловые реакции и перемещения определяются своими компонентами в принятой СК. Для упругой деформации между реакциями и перемещениями существует линейная зависимость

Или в матричной форме ; – вектор узловых реакций; – матрица жесткости КЭ; – вектор узловых перемещений.

Данная система линейных уравнений отражает условия равновесия КЭ.

4)Вывод уравнений для системы в целом.

Уравнения равновесия отдельных КЭ объединяют в одну систему. При этом матрицы жесткости суммируют и получают глобальную матрицу жесткости.

Необходимо также выполнить условия равновесия сил, учесть граничные условия(статические, кинематические). Получим систему линейных для всего тела(конструкции):

[k] * {q}={P}, где {P} и {q} - векторы узловых сил и перемещений всего тела.

[k]-глобальная матрица жесткости.

Матрица [k] имеет размерность nm x nm, где n-число КЭ, а m-число узлов. Она имеет много нулевых элементов. На следующем этапе полученную систему линейных уравнений решают относительно узловых перемещений прямыми или итерационными методами.

5)Решение системы линейных уравнений.

Решение относительно узловых перемещений простыми или итерационными методами.

6)Вычисление значений других величин.

Из полученного распределения перемещений по расчетной области с помощью обычных уравнений теории упругости найдем распределения напряжений и деформаций.