24)Явные и неявные схемы разностной аппроксимации сеточных уравнений. Их преимущества и недостатки. Алгоритм реализации явной схемы на примере решения уравнения теплопроводности.

При решении задач для уравнений параболического и гиперболического типов используются различные разностные схемы, среди которых важное место занимают так называемые явные и неявные разностные схемы. Рассмотрим их на примере классического уравнения параболического типа – уравнения теплопроводности. Задача состоит в отыскании функции u(x,t), удовлетворяющей в области G={(x,t)|0≤x≤l,t>0} уравнению начальному условию u(x,0)=f(x) и граничным условиям u(0,t)=μ₁(t), u(l,t)=μ₂(t).

Математически – это задача Коши с граничными условиями или краевая задача с начальными условиями. Поскольку такую задачу называют эволюционной, имея в виду построение эволюции решения во времени, то её область решения является полубесконечной (t>0). Для проведения численных расчетов ограничим область по оси времени некоторой величиной Т (0<t<T). Решение поставленной задачи будем искать методом сеток с построением разностной схемы. В области решения строим прямоугольную сетку с шагом h в направлении x и τ в направлении t. Координаты узлов обозначим: x_i=i·h, i=0,1,…,n; t_i=j·τ, j=0,1,…,m, где n,m – количество узлов по направлениям х и t, соответственно.

Тогда h= и τ= Искомую сеточную функцию u(x,t) в узлах обозначим u_i,j=u(x_i,t_i). Узлы, имеющие одинаковую временную координату называют t-слоями или слоями по времени.

Решение ищется последовательно по временным слоям, начиная от слоя j=1и далее до слоя j=m включительно. Запишем разностную аппроксимацию с использованием четырехточечных шаблонов двух типов.

Явная схема:

Ui, j+1

Ui-1, j Ui, j Ui+1, j

В явной схеме производная аппроксимируется с использованием известных значений сеточной функции на j-м временном слое. Тогда разностная схема:

Из этого соотношения следует, что искомое значение определяется явным образом через известные значения на j-м слое по соотношению: где параметр λ=

Устойчива только при λ<1/2 или ԏ≤(h²)/2. Вычисления придется вести с очень малым шагом по времени. Число операций значительно меньше.

Неявная схема: Устойчива при любых значениях параметра λ.

U i-1, j+1 Ui, j+1 Ui+1, j+1

Ui, j

Производная аппроксимируется с использованием неизвестных значений сеточной функции на (j+1)-м временном слое. Имеем:

или

Последнее соотношение, записанное для всех внутренних узлов (j+1)-го слоя, порождает систему линейных алгебраических уравнений, с помощью которых определяются неизвестные значения функции в узлах. Каждое уравнение этой системы содержит только три неизвестных, т.е. система обладает трехдиагональной матрицей коэффициентов и её рационально решить либо методом прогонки, либо итерационными методами.

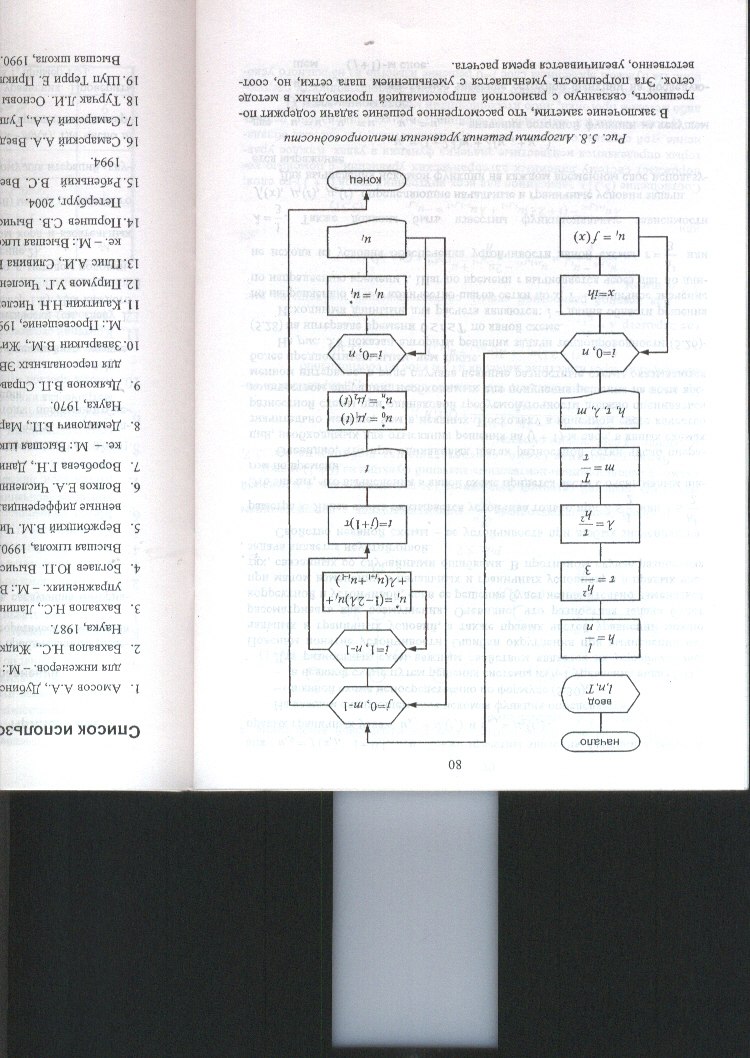
Алгоритм численного решения задачи теплопроводности следующий:

На нулевом временном слое j=0 решение известно из начального условия Ui,0=f(xi), i=0,1,…,n.

Также известны значения функции в левых и правых граничных узлах U0,j=μ1(tj); Un,j=μ2(tj);

В каждом следующем слое искомая функция определяется по формулам соответствующим явной и неявной схемам.

Для выполнения расчетов по разностным схемам важно такое их свойство, как устойчивость. Ошибки округления при вычислении начальных и граничных условий, а так же правых частей уравнений можно рассматривать как возмущения. Очевидно, что разностная задача будет корректной и устойчивой, если её решение будет незначительно изменяться при малом изменении в начальных и граничных условиях, и в правых частях, связанных со случайными ошибками. В противном случае задача является неустойчивой.

Поскольку в конечном счете качество разностной схемы при одинаковой требуемой точности должно оцениваться количеством операций, необходимых для получения решения на всем временном интервале, в ряде случаев неявные разностные схемы оказываются предпочтительнее. Рассмотренное решение задачи содержит погрешность, связанную с разностной аппроксимацией производных в методе сеток. Для её уменьшения нужно уменьшить шаг сетки, но при этом увеличивается время расчета.

Алгоритм реализации явной схемы на примере решения уравнения теплопроводности: