Вынужденные электромагнитные колебания в колебательном контуре.

Е сли к колебательному контуру подключен генератор переменного тока, то его э.д.с. буде вызывать в контуре, то его э.д.с. будет вызывать в контуре вынужденные колебания переменного тока с частотой, равной частоте генератора. При вынужденных колебаниях энергия подводится к контуру непрерывно, благодаря чему эти колебания будут незатухающими, т.о.

Вынужденные колебания – незатухающие колебания заряда , разности потенциалов на обкладках конденсатора, силы тока и других физических величин в колебательном контуре, вызванные периодически изменяющейся синусоидальной э.д.с. , где амплитудное значение э.д.с., циклическая частота переменной э.д.с. К контуру подводится энергия, которая необходима для восстановления потерь энергии в контуре из-за наличия электрического сопротивления .

Тогда дифференциальное уравнение . Решение уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения . Первым членом, характеризующим свободные затухающие колебания в контуре, можно пренебречь по истечении некоторого времени после начала колебаний. Поэтому считаем, что частное решение уравнения имеет вид , где 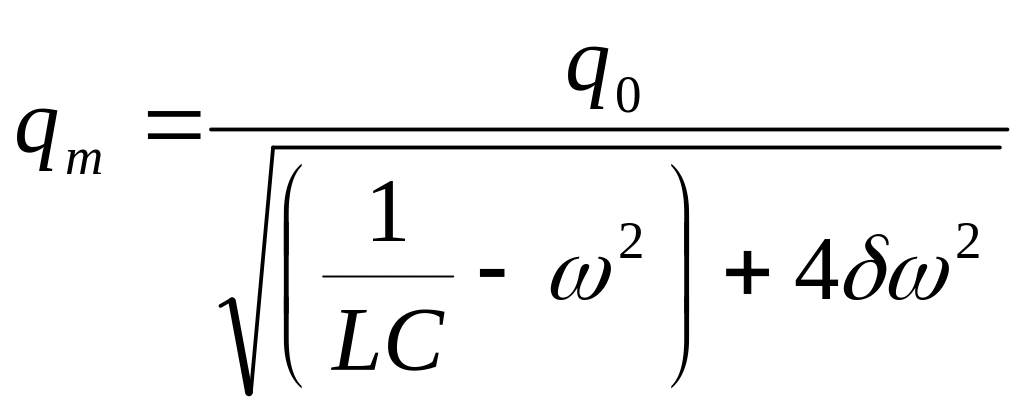, 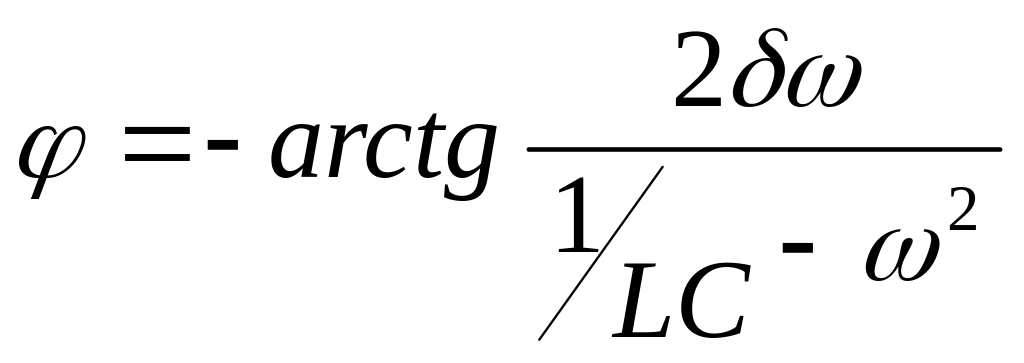- сдвиг фаз между силой тока и приложенной э.д.с. . Сила тока при установившихся вынужденных колебаниях: , где . 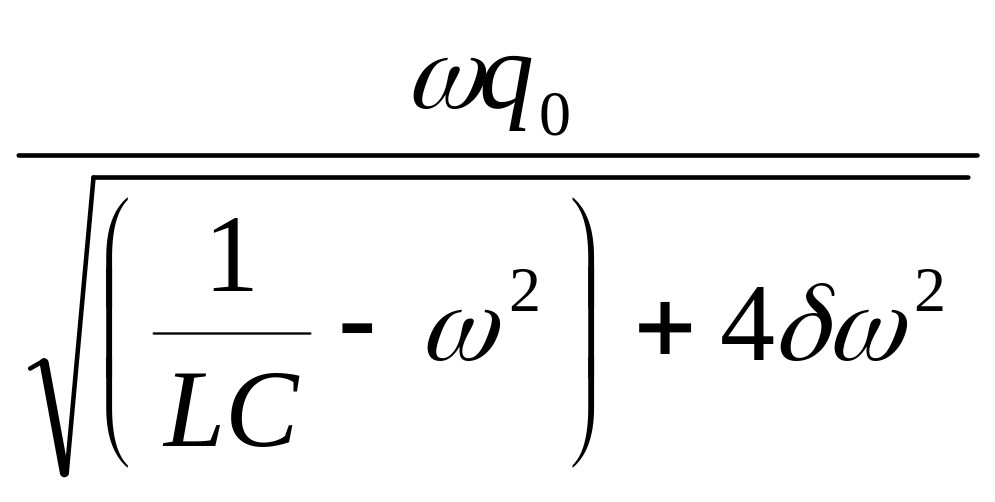Величина называется полным (эффективным) сопротивлением электрической цепи переменного тока (колебательного контура).

Т.к. напряжение на активном сопротивлении, напряжение на конденсаторе, напряжение на индуктивности, то дифференциальное уравнение можно записать в виде - сумма напряжений на отдельных элементах равна в каждый момент времени напряжению, приложенному извне. Тогда ,

, где

, откуда

Чисто индуктивное сопротивление сдвигает фазу силы переменного тока в контуре на сравнительно с фазой приложенной э.д.с. Чисто емкостное сопротивление приводит к опережению по фазе на силы тока сравнительно с э.д.с.

Между амплитудными значениями тока в этой цепи и напряжением на ее конца существует связь, аналогичная закону Ома: или . Эффективные значения тока, напряжения и э.д.с. связаны с их амплитудными значениями соотношениями , , . В этом случае сдвиг фаз между напряжением и током (он равен начальной фазе напряжения) .

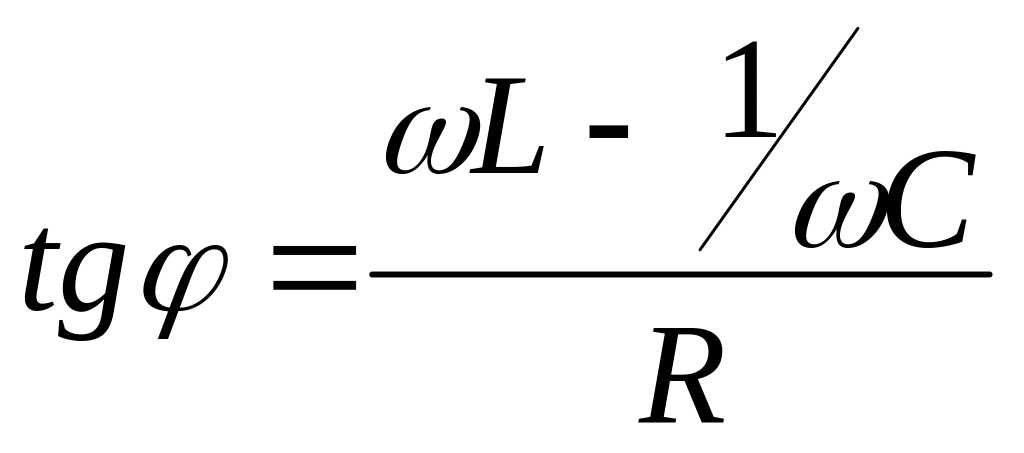А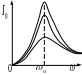 мплитуда вынужденных колебаний зависит от соотношения частот генератора и контура. Она резко возрастает при приближении частоты внешней э.д.с. (генератора) к частоте собственных колебаний контура. Это явление носит название резонанса. Резонансная частота для заряда и напряжения на конденсаторе равна . Резонансные кривые для изображены на рис.1. Они соответствуют резонансным кривым при механических колебаниях. При резонансные кривые сходятся в одной точке с ординатой - напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения . Максимум при резонансе получается тем выше и острее, чем меньше , т.е. чем меньше активное сопротивление и больше индуктивность контура.

Резонансные кривые для силы тока на рис. 2. Они соответствуют резонансным кривым для скорости при механических колебаниях. Амплитуда силы тока имеет максимальное значение при . Следовательно .

П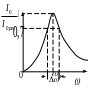 ри этом сила тока . Отрезок, отсекаемый резонансными кривыми на оси равен нулю – при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

При малом затухании , резонансная частота для напряжения , тогда отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения будет равно: добротность контура – показывает, во сколько раз напряжение на конденсаторе может превысить приложенное напряжение. Добротность контура определяет остроту резонансных кривых. На рис. 3 показана одна из резонансных кривых для силы тока в контуре. По вертикальной оси отложены значения . Рассмотрим ширину кривой , взятую на высоте , тогда .

Явление резонанса используется для выделения из сложного напряжения нужной составляющей. Пусть напряжение, приложенное к контуру, равно . Настроив контур на одну из частот (т.е. подобрав соответствующим образом параметры и ), можно получить на конденсаторе напряжение, в раз превышающее значение данной составляющей, в о время как напряжение, создаваемое на конденсаторе другими составляющими, будет слабым. Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.

З адача 4. В цепи, состоящей из последовательно соединенных и конденсатора с емкостью , катушки с индуктивностью и резистора сопротивлением , действует синусоидальная э.д.с. определить 1) частоту э.д.с., при которой в цепи наступит резонанс; 2)найти действующее значение силы тока и напряжений на всех элементах цепи при резонансе, если при этом действующее значение э.д.с. .

Д

Под действием переменной э.д.с. в данной цепи, , представляющей собой колебательный контур, установятся вынужденные электромагнитные колебания. Резонансная циклическая частота ; амплитудные значения тока и э.д.с. связаны соотношением , т. к. и , то .

. ; ;

ано: Решение:

1) ;

2)

,

если

Ответ: ; . ; ; .