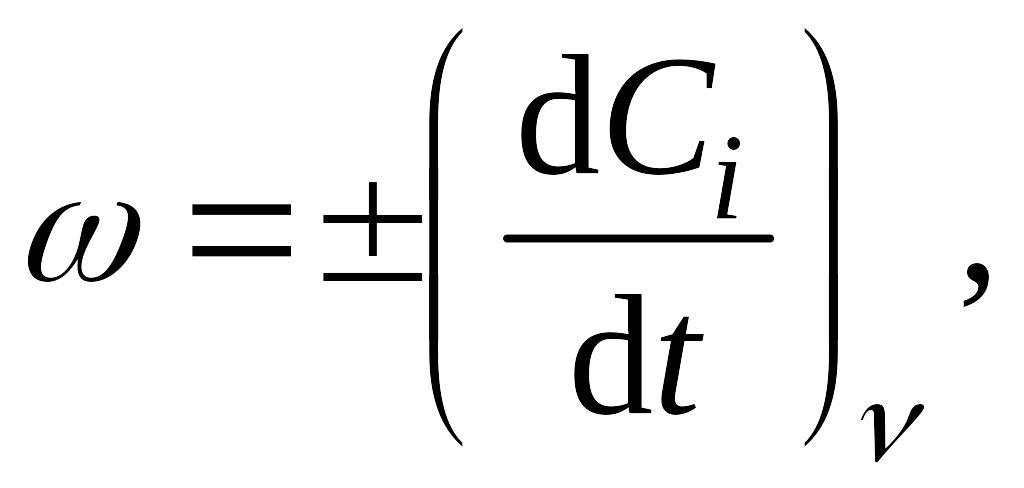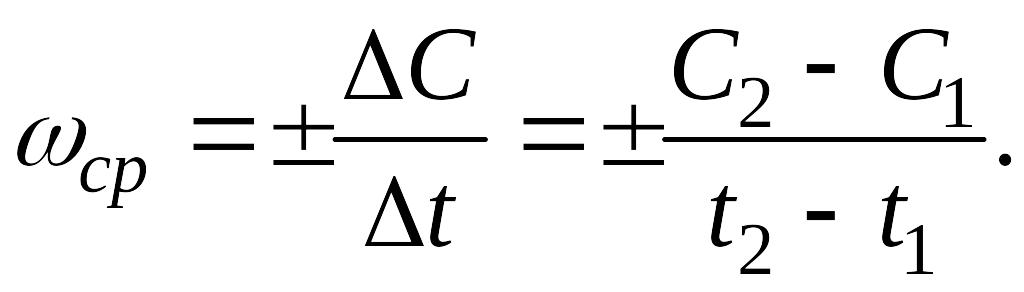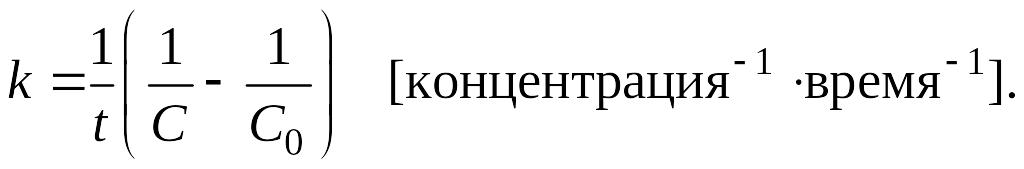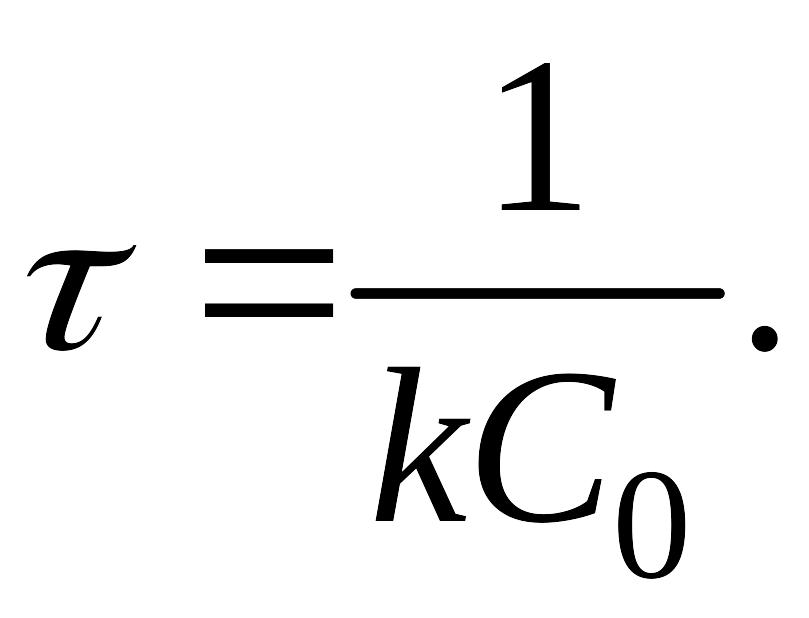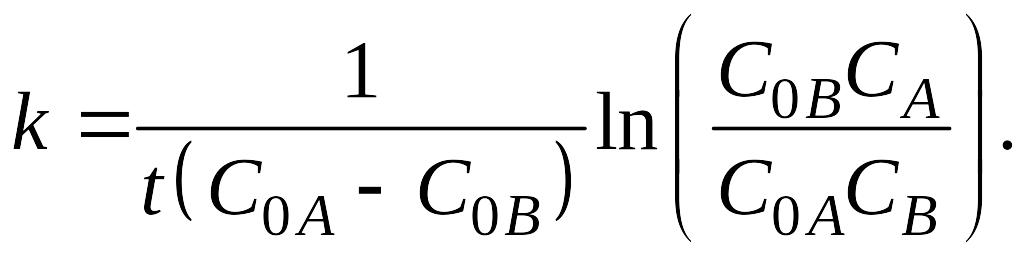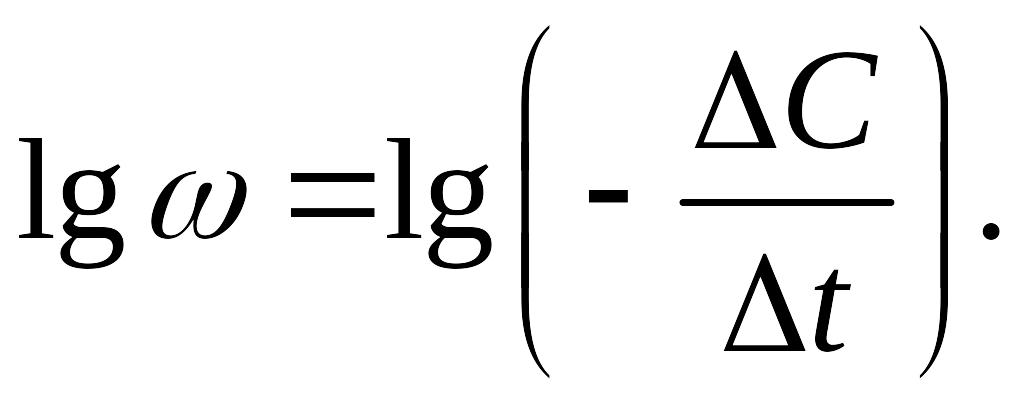Коллоквиум V химическая кинетика теоретическая часть

5.1. скорость химической реакции

5.2. Влияние концентрации на скорость химической реакции

5.3. Зависимость скорости реакции от температуры

5.4. влияние катализатора на скорость реакции

5.5. Кинетика сложных реакций

5.6. Роль кинетических закономерностей в фармацевтической практике

5.1. Скорость химической реакции

Направление химической реакции можно определить с помощью химической термодинамики. Однако химическая термодинамика не позволяет установить продолжительность химической реакции или предсказать, осуществима ли она вообще. Есть немало примеров самопроизвольного протекания химических реакций с точки зрения химической термодинамики, которые на практике не реализуемы без внешнего воздействия. Например, смесь газообразных водорода и кислорода термодинамически неустойчива и должна самопроизвольно прореагировать с образованием воды. Тем не менее эту смесь можно наблюдать очень долго, при этом, мы не обнаружим образование воды. Определить реальность протекания химических реакций во времени позволяет химическая кинетика.

Химические реакции протекают с различной скоростью. Учение о скорости, механизме химических реакций и их зависимости от разных факторов (концентрации, температуры, катализатора и т. д.) называется химической кинетикой.

Скорость химической реакции в газах и растворах определяется изменением концентрации любого из реагентов, принимающих участие в процессе, в единицу времени в единице объема:

(5.1)

где ω  скорость реакции;  бесконечно малое изменение концентрации i-го компонента за бесконечно малый промежуток времени dt при постоянном объеме. Размерность скорости реакции: концентрация  время^1. Знак минус справа ставится при определении скорости реакции по одному из исходных веществ.

Скорость реакции в данный момент времени (истинная скорость) можно рассчитать графически по кинетической кривой изменения концентрации, или какого-то физического свойства вещества, пропорционального концентрации, от времени. Для этого проводят касательную к кинетической кривой, и скорость реакции (согласно (5.1)) будет равна тангенсу угла наклона касательной к кривой в данной точке: ω = tg α = AB/BC (рис. 5.1). Чтобы правильно провести касательную, можно использовать следующий приём. Небольшое зеркало ставят перпендикулярно плоскости рисунка так, чтобы отраженная в зеркале часть кривой была плавным продолжением кривой на рисунке. Затем вдоль зеркала проводят прямую. Перпендикуляр к этой прямой, проведенный через выбранную точку, и будет касательной.

Рис. 5.1. Определение скорости реакции по кинетической кривой

Средняя скорость реакции характеризует изменение концентрации за определенный конечный промежуток времени:

(5.2)

5.2. Влияние концентрации на скорость химической реакции

Основным законом химической кинетики является постулат, вытекающий из большого числа экспериментальных данных и выражающий зависимость скорости реакции от концентрации реагентов. Скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций реагирующих веществ, возведенных в некоторые степени (закон действующих масс).

Для реакции

(5.3)

скорость процесса по каждому из реагирующих веществ определяется следующим образом:

(5.4)

где k – константа скорости реакции.

Физический смысл k легко установить, приняв C_A = C_B = 1 моль/л. Тогда ω=k, т. е. константа скорости равна скорости реакции при концентрации реагирующих веществ равных единице.

Выражение (5.4) есть математическая формула, связывающая скорость реакции с концентрациями. Она называется кинетическим уравнением.

При изучении кинетики химические реакции классифицируют по молекулярности и порядку. Молекулярностью реакции называется число частиц, принимающих участие в одном элементарном акте химического превращения. Реакции бывают мономолекулярными, бимолекулярными, реже тримолекулярными.

Порядок реакции n равен сумме показателей степеней концентраций всех реагентов, которые входят в кинетическое уравнение для скорости реакции. Для реакции (5.3) (согласно уравнению (5.4)) порядок реакции будет следующий:

(5.5)

Показатель степени, в которой концентрация вещества входит в кинетическое уравнение, называется порядком реакции по данному веществу. Для элементарной реакции (5.3) a и b являются частными порядками по веществу A и B. Порядок реакции совпадает с молекулярностью, если она протекает за один элементарный акт.

Порядок реакции может быть положительным, целым, дробным и нулевым. В зависимости от этого выражение для константы скорости будет различным.

Каждый тип реакции описывается определенным кинетическим уравнением, связывающим концентрации со временем.

Для реакции нулевого порядка (n=0)

(5.6)

где С₀ – исходная концентрация реагента; С – концентрация реагента в момент времени t.

Большинство известных реакций нулевого порядка представляют собой гетерогенные процессы, например, разложение на платиновой проволоке оксида азота (I)

или аммиака

Для реакции первого порядка (n=1) типа А → продукты кинетическое уравнение и выражение для константы скорости 1-го порядка имеют вид:

(5.7)

Время, за которое исходная концентрация вещества уменьшается наполовину, называется периодом полураспада (τ). Для реакций первого порядка период полураспада

(5.8)

Таким образом, в реакциях первого порядка, время полураспада не зависит от количества исходного вещества, следовательно, за единицу времени распадается одна и та же часть вещества независимо от исходной концентрации. Так, если в первые 15 мин в реакцию вступило 5 % взятого вещества, то за следующие 15 мин распадутся еще 5 % оставшегося.

Примером необратимых реакций 1-го порядка служит разложение диметилового эфира

или разложение азометана

Для реакций второго порядка (n=2) типа А + В → продукты закон действующих масс запишется:

(5.9)

При решении уравнения (5.9) различают два случая:

1) начальная концентрация реагентов одинакова: С_0А=С_0В=С₀. Кинетическое уравнение имеет вид

(5.10)

Решение этого уравнения дает выражение для константы скорости 2-го порядка:

(5.11)

Период полураспада веществ А и В одинаков и равен:

(5.12)

К реакциям данного типа относятся:

газофазное разложение иодоводорода

или разложение оксида азота (IV)

2) начальная концентрация веществ А и В различна: С_0А ≠ С_0В.

В этом случае решение уравнения (5.9):

(5.13)

Периоды полураспада исходных веществ будут различными:

Этот случай реализуется в следующих реакциях.

Газофазное образование иодоводорода

Омыление этилацетата раствором гидроксида натрия

Для того чтобы определить такой важный параметр химической реакции, как константа скорости, необходимо предварительно установить порядок реакции, который в отличие от молекулярности является величиной формальной и его нельзя предсказать даже для реакций, сходных между собой. Для определения порядка реакции необходимо иметь экспериментальные данные об изменении концентрации реагирующих веществ во времени. Рассмотрим наиболее часто применяемые методы определения порядка реакции.

1. Метод интегрирования (метод подстановки). Он заключается в определении концентрации реагента в различные моменты времени и подстановке полученных данных в кинетические уравнения различных порядков. Уравнение, в соответствии с которым рассчитанная константа скорости для различных интервалов времени почти не изменяется, следует считать наиболее правильно отражающим порядок реакции.

2. Метод графической подстановки заключается в построении графиков, выражающих зависимость различных функций концентрации (в соответствии с порядком реакции) от времени. График, на котором наблюдается линейная зависимость, свидетельствует о соответствующем порядке реакции.

Для реакции нулевого порядка, в соответствии с кинетическим уравнением (5.6), при построении графика зависимости концентрации от времени (C=f(t)) получится прямая линия.

Если прямая получается в координатах или lnC=f(t), то эта реакция в соответствии с уравнением (5.7) 1-го порядка.

Для реакции 2-го порядка линейная зависимость будет наблюдаться в координатах , при условии равенства концентраций исходных реагентов.

3. Графический метод. Реакцию проводят при одинаковых концентрациях реагирующих веществ. Выражение для скорости реакции логарифмируют и строят график в координатах lgω=f(lgC) (рис. 5.2):

		(5.14)
		(5.15)
где

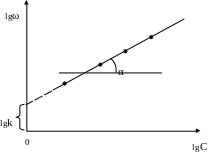
Рис. 5.2. Графическое определение общего порядка реакции

Тангенс угла наклона прямой равен общему порядку реакции n: n = tgα, а отрезок, отсекаемый на оси ординат, равен lgk.