19. Способы получения поляризованного света.

Способы получения поляризованного света:

1. отражение и преломление света на границе двух прозрачных изотропных диэлектриков (использование закона Брюстера);

2. пропускание света через среды, обладающие оптической анизотропией (двойного лучепреломления)

а) естественной,

в) вызванной внешними воздействиями;

3. поляризовано излучение лазеров.

1. Поляризация света при отражении и преломлении на границе двух диэлектриков

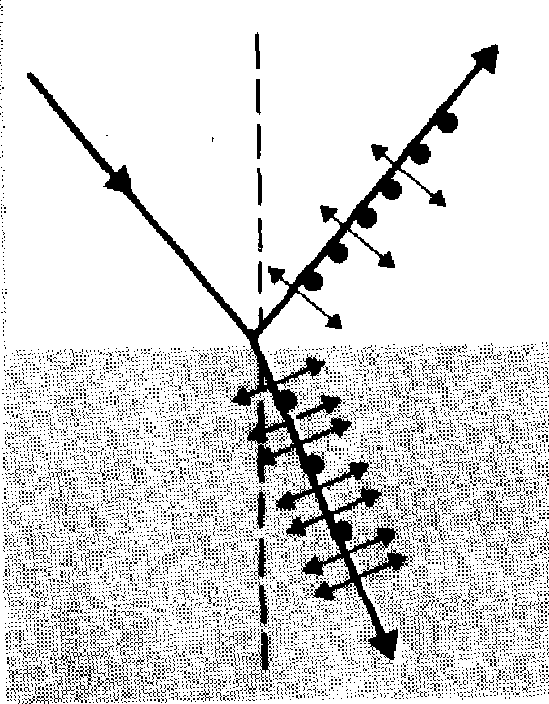
Пусть естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла): часть его отражает­ся, часть преломляется и распространя­ется во второй среде. Отраженный и прелом­ленный лучи частично поляризованы. В отраженном луче преобла­дают колебания, перпендикулярные плоскости падения (на рис. они обоз­начены точками), в преломленном — коле­бания, параллельные плоскости падения (изображены стрелками).

Степень поляризации зависит от угла падения лучей и показателя преломления.

Ш

отландский физик Д. Брюстер установил закон, названный его именем:

Закон Брюстера: при угле паде­ния (угол Брюстера), определяемого со­отношением

(19.1)

( — показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (со­держит только колебания, перпендикуляр­ные плоскости падения). Преломленный луч при угле падения по­ляризуется максимально, но не полностью.

Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендику­лярны.

Степень поляризации отраженного и преломленного света при различных уг­лах падения можно рассчитать из уравне­нии Максвелла, если учесть граничные ус­ловия для электромагнитного поля на гра­нице раздела двух изотропных диэлектри­ков (так называемые формулы Френеля).

Степень поляризации преломленного света может быть значительно повышена (многократным преломлением при условии падения света каждый раз на границу раздела под углом Брюстера). Если, на­пр., для стекла (n=1,53) степень по­ляризации преломленного луча составляет ~15%, то после преломления на 8—10 наложенных друг на друга стеклянных пластинок вышедший из такой системы свет будет практически полностью поляри­зованным. Такая совокупность пластинок называется стопой.

О пр. 19.1. Стопа – совокупность наложенных друг на друга стеклянных пластинок, при прохождении которых луч света становится практически полностью поляри­зованным.

Стопа может служить для анализа поляризованного света как при его отражении, так и при его пре­ломлении.

2. А. Пропускание света через среды, обладающие естественной оптической анизотропией.

Двойное лучепреломление.

В предыдущих лекциях, рассматривая закономерности распространения света в различных средах, мы предполагали, что среда оптически изотропна, т.е. скорость света в каждой точке среды не зависит ни от направления распространения световой волны, ни от характера поляризации волн. Исследования показали, что при обычных условиях газообразные, жидкие и твердые аморфные диэлектрики оптически изотропна. В то же время практически все кристаллические диэлектрики оптически анизотропны. Оказалось так же, что под влиянием внешних воздействий среда, бывшая оптически изотропной, может стать оптически анизотропной. Это явление наз. искусственной оптической анизотропией, которое имеет большое практическое значение и будет рассмотрено ниже.

Закономерности распространения света в любой среде в конечном счете определяются интерференцией первичной волны и вторичных волн, излучаемых молекулами, атомами или ионами среды вследствие их электронной поляризации под действием электрического поля световой волны. Поэтому оптические свойства среды полностью обусловлены электрическими свойствами этих элементарных излучателей, их взаимным расположением и взаимодействием друг с другом. Но электрические свойства частиц еще не определяют полностью оптические свойства среды, т.к. при обычных условиях частицы в газообразных, жидких и твердых аморфные диэлектриках ориентированы хаотически. Если среда находится в кристаллическом состоянии, то ее частицы (атомы, молекулы или ионы) располагаются в строгом порядке, образуя кристаллическую решетку. Каждая частица находится в сильном взаимодействии с ближайшими соседями в решетке. Поэтому излучение вторичных волн частицами кристаллической среды зависит не только от электрических свойств самих частиц, но и от силового воздействия со стороны других частиц (зависит от степени симметрии решетки кристалла). Как показали исследования, только кристаллы кубической системы, обладающие высокой степенью симметрии решетки, являются оптически изотропными. Все остальные кристаллы независимо от электрических свойств образующих их частиц оптически анизотропны.

Расчет интерференции вторичных волн в анизотропных кристаллах весьма сложен. Более простой метод изучения распространения света основывается на применении теории Максвелла для переменного электромагнитного поля: кристалл – однородная среда, диэлектрическая проницательность которой (считая ) неодинакова в различных направлениях. Оптическая анизотропия немагнитных кристаллов явл. следствием анизотропии относительной диэлектрической проницательности.

С помощью уравнений Максвелла можно установить важную особенность распространения света в анизотропных средах: в анизотропном кристалле всякая плоская монохроматическая световая волна распадается на две плоские волны, которые линейно поляризованы во взаимно перпендикулярных плоскостях и обладают различными скоростями.

Все прозрачные кристаллы (кроме кристаллов кубической системы, которые оптически изотропны) обладают способно­стью двойного лучепреломления, т. е. раздваивания каждого падающего на них светового пучка. Эти лучи распространяются с разными скоростями и в различных направлениях. Это явление, в 1669 г. впервые обнаруженное датским ученым Э. Бартолином (1625—1698) для исландского шпата (разновидность каль­цита СаСОз), объясняется особенностями распространения света в анизотропных средах и непосредственно вытекает из уравнений Максвелла. Рассмотрим анизотропный кристалл.

Опр. 19.2. Направление в оптически анизот­ропном кристалле, по которому луч света, падающий нормально на плоскую поверхность кристалла, распространяется не испытывая двойного лучепреломления, называется оптической осью кристалла.

В данном случае речь идет именно о направлении. Любая прямая, проходящая параллельно данному направлению, явля­ется оптической осью кристалла. Кристал­лы в зависимости от типа их симметрии бывают одноосные и двуосные, т. е. имеют одну или две оптические оси (к первым относится исландский шпат, кварц и турмалин).

О пр.19.3. Плоскость, проходящая через направ­ление луча света и оптическую ось кристалла, называется главной плоско­стью (или главным сечением кристалла).

Двойное лучепреломление объясняется анизотропией кристаллов – диэлектрическая постоянная оказывается зависящей от направления. В одноосных кристаллах в направлении оптической оси и в направлениях, перпендикулярных к ней, имеет различные значения и . В других направлениях имеет промежуточные значения. Но - э/м волнам с различными направлениями колебаний вектора Е соответствуют разные значения и . В одном из лучей колебания светового вектора происходят в направлении, перпендикулярном к главному сечению кристалла – Е образует с оптической осью прямой угол и постоянна. В другом луче колебания совершаются в главном сечении - Е образует с оптической осью различные углы.

Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу.

Опр. 19.4. При двойном лучепреломлении преломленный луч, подчиняющийся обычному закону преломления наз. обыкновенным (о).

1. лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности;

2. показатель преломления n₀ для него есть величина постоянная;

3. луч распространяется по всем направлениям с одинаковой скоростью ;

4. луч плоско поляризован, колебания светового вектора происходят перпендикулярно главной плоскости.

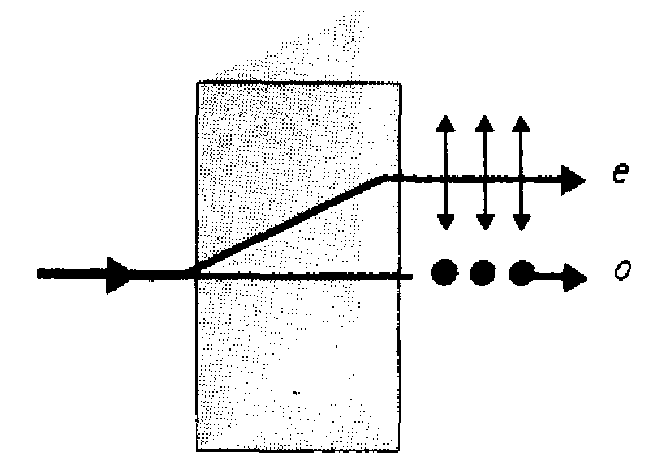
Опр. 19.5. При двойном лучепреломлении преломленный луч, не подчиняющийся обычному закону преломления наз. необыкно­венным (е).

1. показатель преломления яв­ляется переменной величиной, зависящей от направления луча.

2. лучи распространяются по различным направлениям с разными скоростями в зависимости от угла между вектором Е и оптической осью;

3. луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности.

4. луч плоско поляризован, колебания светового вектора в необыкновенном луче происходят в главной плоскости.

Для луча, распространяющегося вдоль оптической оси . Наибольшее расхождение этих значений наблюдается в направлении, перпендикулярном оптической оси.

Даже в том случае, когда первичный пучок пада­ет на кристалл нормально, преломленный пучок разделяется на два, причем обыкновенно­го является продолжением первичного, а необыкно­венного отклоняется от нормали.

Если , то одноосный кристалл наз. положительным; если - отрицательным.

Замечание: после выхода из кристалла, если не принимать во внима­ние поляризацию во взаимно перпендику­лярных плоскостях, эти два луча ничем друг от друга не отличаются, так что названия «обыкновенный» и «необыкновенный» имеют смысл только внутри кристалла.

В двуосном кристалле оба преломленных луча явл. необыкновенными.