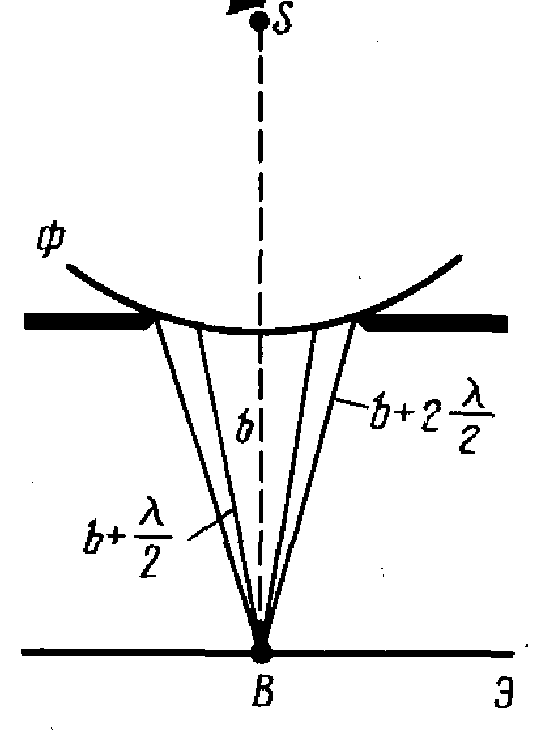
13. Дифракция сферических волн.

Дифракция сферических волн (дифракция Френеля) - дифракци­онная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию. Обычно рассчитывается графически.

1

. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием радиуса . Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром отверстия. b-расстояние от вершины волновой поверхности до т. В, а- радиус волновой поверхности.

Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии:.

• в отсутствие непрозрачного экрана с отверстием в т. В амплитуда

• в отверстие уклады­вается нечетное число m зон Френеля, в т. В амплитуда больше, чем в отсутствие непрозрачного экрана. Напр., если в отверстие уклады­вается одна зона Френеля, в т. В амплитуда А=А₁, вдвое больше, чем в отсутствие непрозрачного экрана (интенсивность света больше в четыре ра­за) – наблюдается максимум.

• в отверстие уклады­вается четное число m зон Френеля, в т. В амплитуда меньше, чем в отсутствие непрозрачного экрана. Напр., в отверстии укладываются две зоны Френеля, в т. В амплитуда (волны практически уничтожат друг друга из-за интерференции) – наблюдается минимум.

1. Дифрак­ционная картина от круглого отверстия вблизи точки В будет иметь вид чередую­щихся темных и светлых колец с центрами в точке В (если m четное, то в центре будет темное кольцо, если т нечетное — то светлое кольцо), причем интенсивность максимумов убывает с расстоянием от центра картины.

2. Если отверстие освещается не монохроматическим, а бе­лым светом, то кольца окрашены.

3. Число зон Френеля, укладывающихся в отверстии. Если и и радиус удовлетворяет условию (12.3), то отверстие оставит открытым (13.1)

4. Если диаметр отверстия велик - интерференционной картины не будет – свет будет распространяться почти так же, как в отсутствии экрана – прямолинейно, (точнее: чередование темных и светлых колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной).

Замечание: Расчет произведен для точки, лежащей против центра отверстия. Расчет амплитуды результирующих колебаний в других точках участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном.

П равомерность деления волнового фронта на зоны Френеля подтверждена экспериментально при помощи зонных пластинок – стеклянных пластинок, состоящих из системы чередующихся прозрачных и непрозрачных колец, построенных по принципу расположения зон Френеля.

В

еличину можно сделать очень большой при помощи зонной пластинки, в которой непрозрачное покрытие закрывает все четные зоны Френеля и оставляет открытыми все нечетные зоны. Если общее число зон, умещающихся на пластинке, равно , то . Если не слишком велико, то и освещенность экрана в т. В в раз больше, чем при беспрепятственном распространении света от источника в т. В.

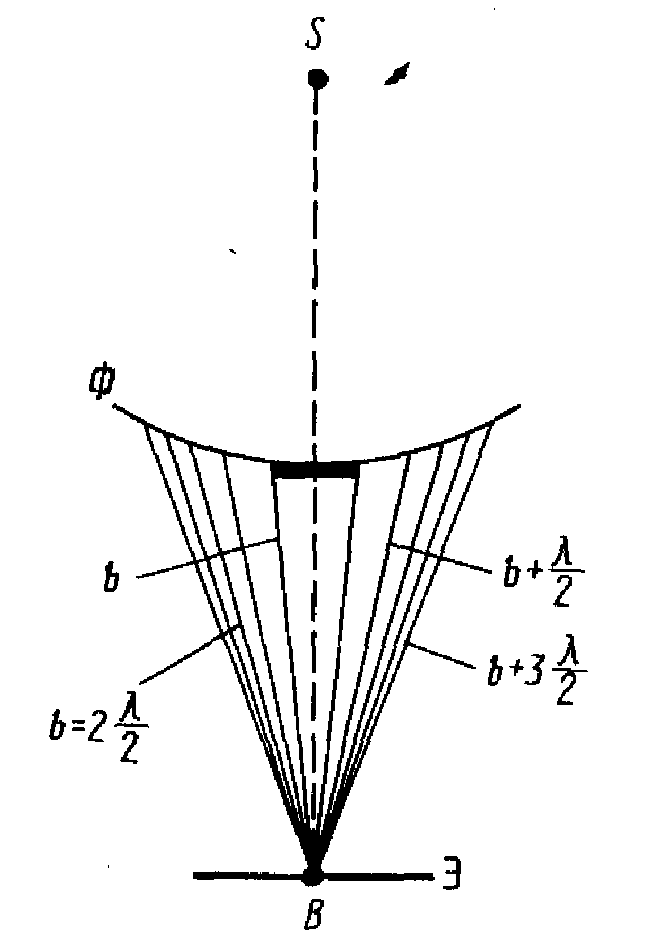
2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска. Закрытый диском участок фронта волны надо исклю­чить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля.

1. В точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствую­щий половине действия первой открытой зоны Френеля .

2. Центральный максимум ок­ружен концентрическими темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины. С увеличением радиуса диска первая открытая зона Френеля удаляется от т. S и увеличивается угол между нормалью к поверхности этой зоны и направлением на т. В.

3. С увеличением размеров диска интенсивность центрального мак­симума уменьшается.

4. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место слабая дифракционная картина - свет распространяющимся почти пря­молинейно.

Замечание: Если форма краев экранов и отверстий в них от­личается от геометрически идеальной, то дифракционные закономерности не выполняются. Степень отклонения от этих закономерностей определяется вели­чиной , где —длина основания или высота вы­ступов (шероховатостей) на краях экрана, b—расстоя­ние от экрана до точки наблюдения, —длина волны:

а) < 1 — нарушения дифракционной картины практически отсутствуют;

б) ~1—дифракционная картина сглаживается и может исчезнуть;

в) >1—дифракционные полосы или кольца по­вторяют конфигурацию выступов и впадин на внешних краях экранов или краях отверстий в них.