
- •Лекция 6.
- •Глава 3. Основы молекулярной физики и термодинамики.
- •§1.Основные понятия.
- •Внешние.
- •Внутренние.
- •§2.Законы идеальных газов.
- •Р Дано: , , , ешение:
- •Р Дано: ешение:
- •Р Дано: , , , , , ешение:
- •Р Дано: , , ешение:
- •§3.Молекулярно-кинетическая теория газов.
- •Распределение частиц во внешних полях.
- •Опытное обоснование молекулярно-кинетической теории.
- •Р Дано: , , , , ешение:
- •Р Дано: ешение:
- •Р Дано: , , ешение:
- •Лекции 7-8.
- •§4.Физические основы термодинамики. Внутренняя энергия системы.
- •Теплообмен. Явления переноса.
- •Вакуум и методы его получения.
- •Работа.
- •Первый закон термодинамики.
- •Р Дано: , , ешение:
- •Решение:
- •Обратимые и необратимые процессы.
- •Энтропия.
- •Круговые процессы. Цикл Карно.
- •Второй закон термодинамики.
- •Третий закон.
- •Р Дано: , , , , ешение:
- •Р Дано: , , , ешение:
- •Решение:
- •Решение:
- •Решение:
- •§5.Реальные газы. Жидкости. Реальные газы.
- •Изотермы реальных газов.
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
Вакуум и методы его получения.
Опр.
3.4.3. Вакуумом называется
состояние газа, при котором средняя
длина свободного пробега
![]() сравнима или больше характерного
линейного размера
сравнима или больше характерного
линейного размера
![]() сосуда. В котором газ находится.
сосуда. В котором газ находится.
Виды вакуума:
низкий
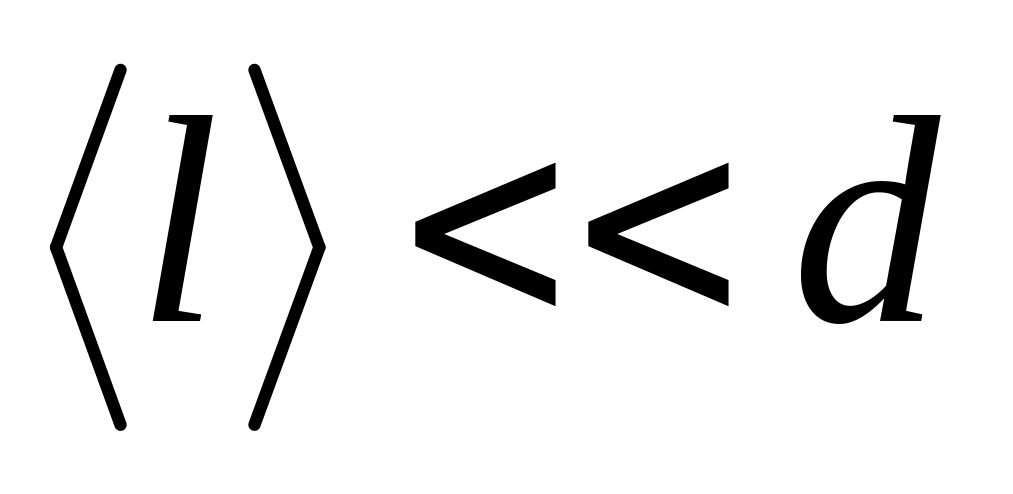 ;
;средний
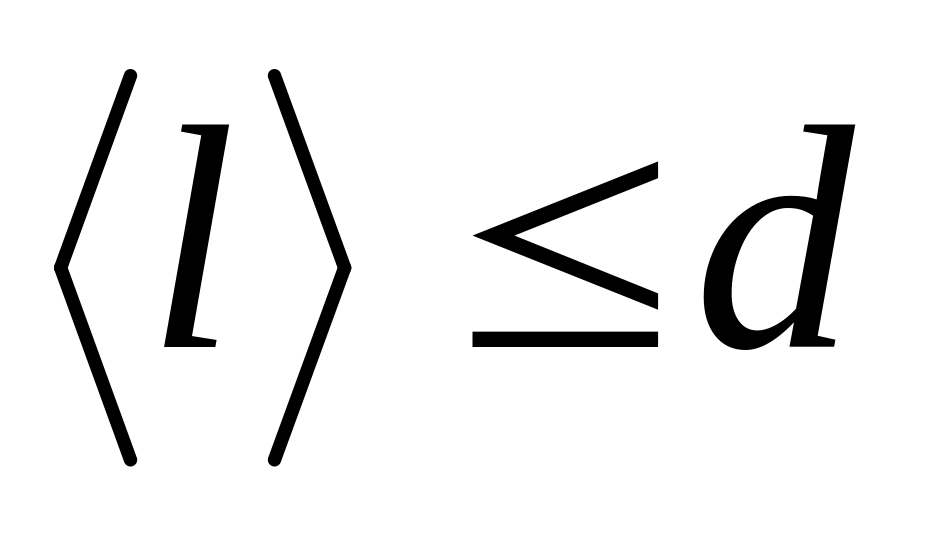 ;
;высокий
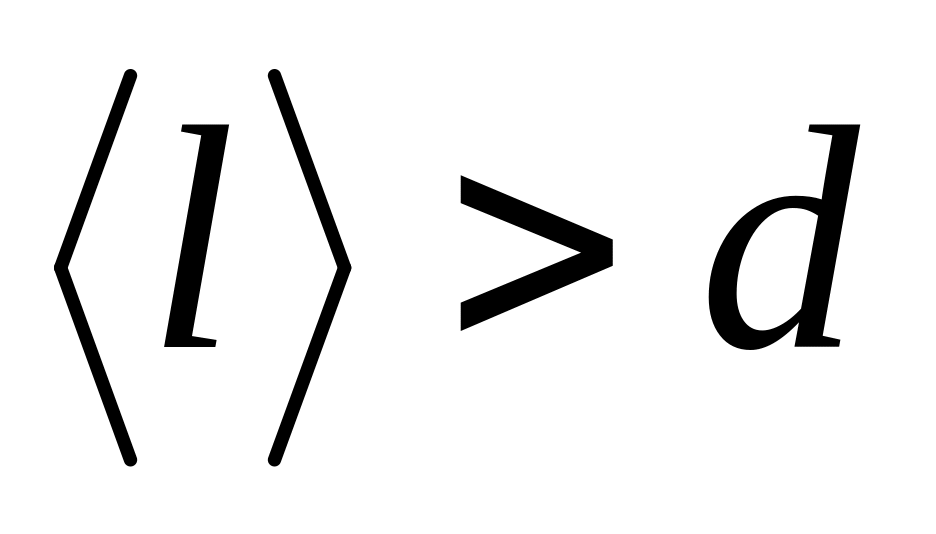 ;
;сверхвысокий
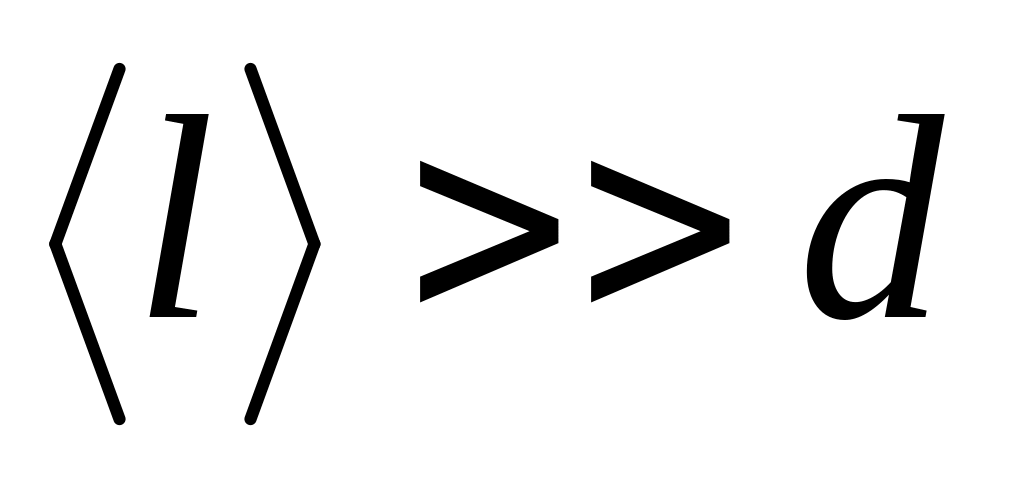 .
Газ в этом
состоянии наз. ультраразреженным.
Используются
для создания тепловой изоляции.
.
Газ в этом
состоянии наз. ультраразреженным.
Используются
для создания тепловой изоляции.
Методы получения вакуума:
вакуумные насосы
диффузионные насосы (рабочее вещество – ртуть или масло)-для получения высокого вакуума, применяют вместе с форвакуумными насосами
Опр. 3.4.3. Теплоемкость есть физическая величина, численно равная теплоте, необходимой для нагревания тела (системы) на один кельвин:
![]() ,
(3.4.3.)
,
(3.4.3.)
где
![]() теплота,
подведенная к телу при повышении его
температуры на
теплота,
подведенная к телу при повышении его
температуры на
![]() .
.
Опр.3.4.4.
Теплоемкостью (истинной
теплоемкостью) C
тела называется
отношение элементарного количества
тепла![]() ,
сообщенного телу в каком-либо процессе,
к соответствующему изменению температуры
тела:
,
сообщенного телу в каком-либо процессе,
к соответствующему изменению температуры
тела:
![]() .
(3.4.4.)
.
(3.4.4.)
Теплоемкость зависит от массы тела, его химического состава, термодинамического состояния и вида процесса сообщения тепла.
Опр.
3.4.5. Киломольная
(молярная) теплоемкость
есть физическая
величина, численно равная теплоте,
необходимой для нагревания одного
киломоля вещества на 1 К:
![]() .
(3.4.5.)
.
(3.4.5.)
Молярная
теплоемкость смеси газов, состоящей из
![]() компонентов:
компонентов:
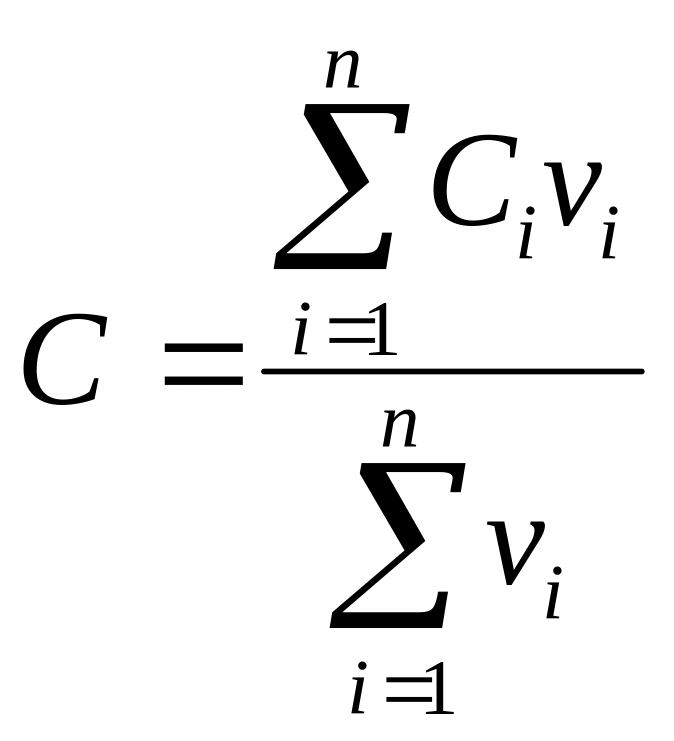 .
(3.4.6.)
.
(3.4.6.)
Опр.3.4.6.
Удельной теплоемкостью
с
называется
теплоемкость единицы массы однородного
вещества. Измеряется
количеством теплоты, необходимой для
нагревания единицы массы вещества на
1К:![]() .
(3.4.7.)
.
(3.4.7.)
Удельная теплоемкость смеси газов, состоящей из компонентов:
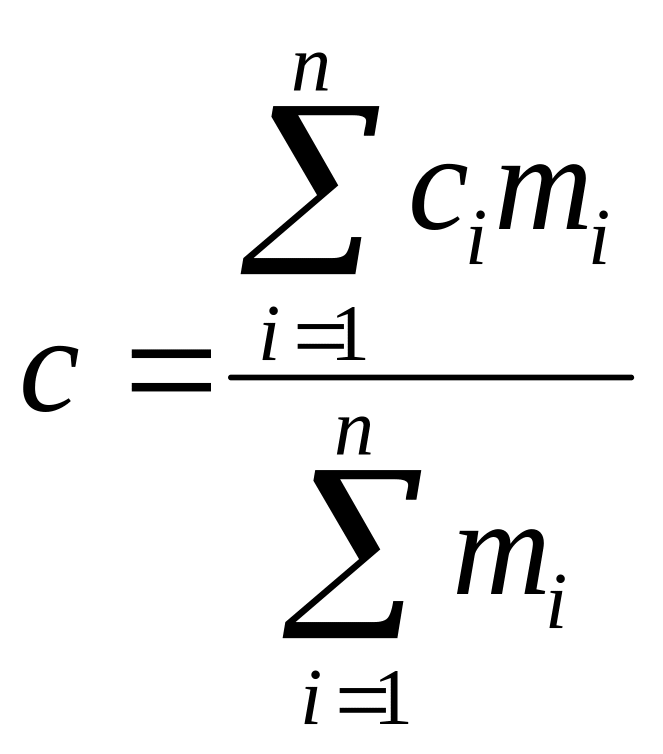 .
(3.4.8.)
.
(3.4.8.)
Для
однородного тела массы
![]() ,
(3.4.9.)
,
(3.4.9.)
Киломольная
теплоемкость
и удельная теплоемкость
![]() связаны соотношением
связаны соотношением
![]() .
(3.4.9’.)
.
(3.4.9’.)
Опр.3.4.7. Средней теплоемкостью С тела в интервале температур от T1 до Т2 > T1 называется отношение тепла Q, необходимого для повышения температуры тела от T1 до Т2 к разности температур Т2 - T1:
![]() (3.4.10.)
(3.4.10.)
Элементарное
количество тепла
![]() ,
сообщаемое телу для изменения его
температуры от Т до
,
сообщаемое телу для изменения его
температуры от Т до
![]() ,
равно
,
равно![]()
Теплоемкость газов различна в зависимости от процесса. Поэтому различают:
теплоемкость газа при постоянном объеме. Молярная теплоемкость
 ,
(3.4.11.)
,
(3.4.11.)
удельная
теплоемкость
![]() .
(3.4.11’.)
.
(3.4.11’.)
теплоемкость газа при постоянном давлении. Молярная теплоемкость
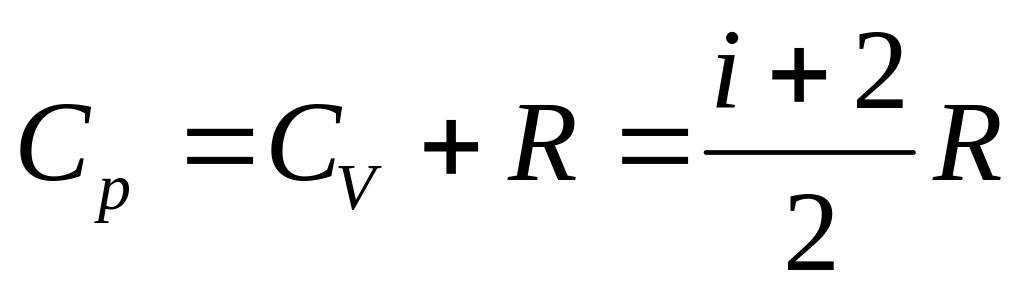 ,
(3.4.12.)
,
(3.4.12.)
удельная
теплоемкость
![]() .
(3.4.13’.)
.
(3.4.13’.)
Отношение
![]() теплоемкости газа при постоянном
давлении к теплоемкости его при постоянном
объеме:
теплоемкости газа при постоянном
давлении к теплоемкости его при постоянном
объеме:
![]() .
(3.4.14.)
.
(3.4.14.)
Уравнение
Роберта Майера.
Разность
киломольных теплоемкостей газов при
постоянном давлении и постоянном объеме
равна универсальной газовой постоянной:
![]() .
(3.4.15.)
.
(3.4.15.)
Внутренняя
энергия
идеального
газа равна сумме средних кинетических
энергий всех молекул, входящих в состав
газа:![]() ,
(3.4.16.)
,
(3.4.16.)
где
![]() средняя кинетическая энергия одной
молекулы.
средняя кинетическая энергия одной
молекулы.
Внутренняя
энергия
идеального
газа
пропорциональна
абсолютной
температуре и определяется по формуле
![]() (3.4.17.)
(3.4.17.)
или
![]() ,
(3.4.17’.)
,
(3.4.17’.)
где
![]() теплоемкость
одного киломоля газа при постоянном
объеме.
теплоемкость
одного киломоля газа при постоянном
объеме.
