Распределение частиц во внешних полях.

П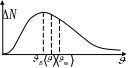 о молекулярно-кинетической теории, как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой в газе, находящемся в состоянии равновесия, остается постоянной . Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. При выводе закона распределения максвелл предполагал, что газ состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Силовые поля на газ не действуют.

Закон распределения Максвелла (распределение молекул идеального газа по скоростям). Число молекул, относительные скорости которых находятся в интервале от до , определяется по формуле

, (3.3.8.)

где общее число молекул, интервал относительной скорости. Формула справедлива, если .

Скорость молекул:

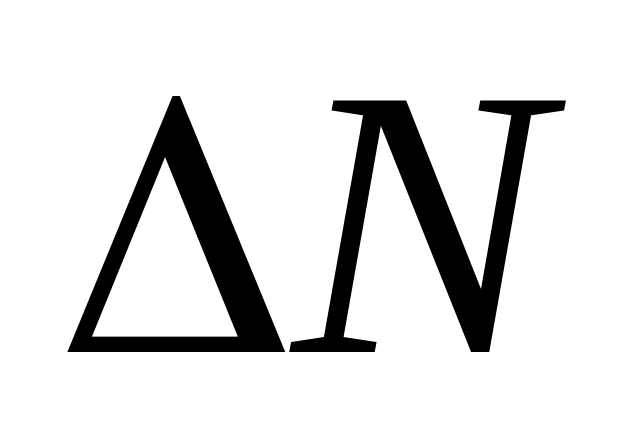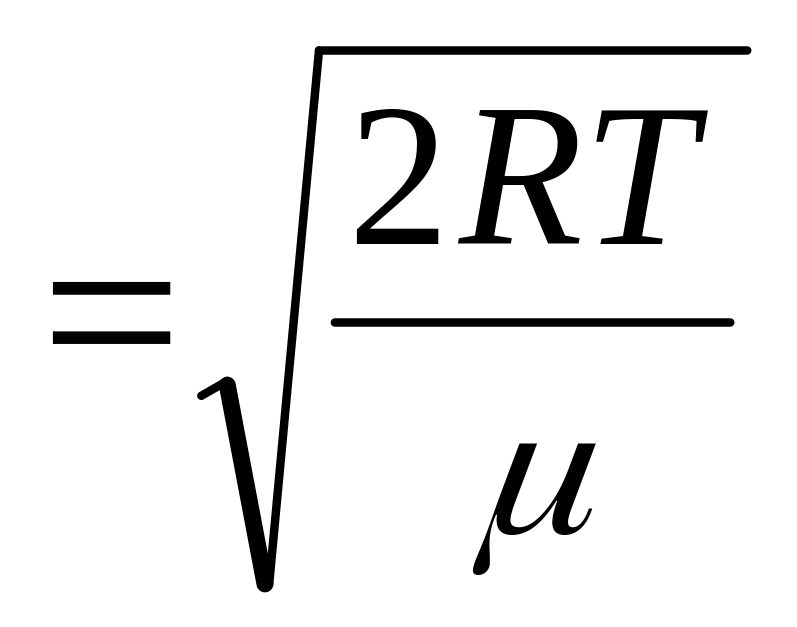• наиболее вероятная – скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, т.е. продифференцируем функцию по и найдем скорость при . Получаем , (3.3.14.)

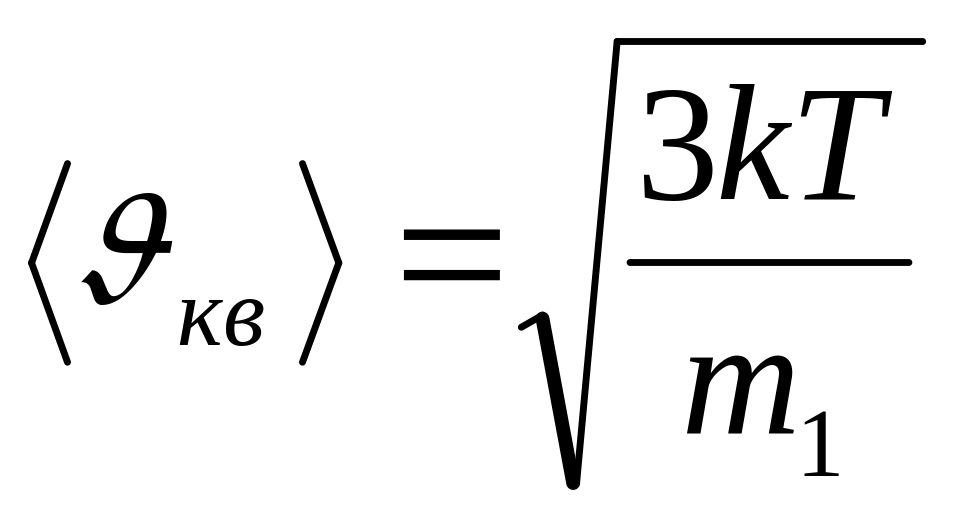
• средняя квадратичная , (3.3.12.)

где масса одной молекулы,

• средняя арифметическая – определяется по формуле 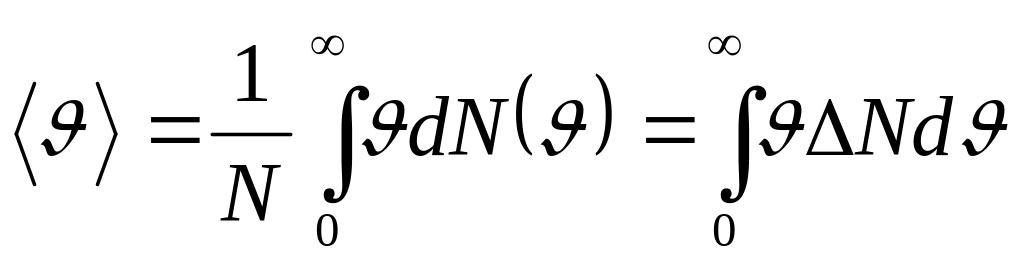. Подставляя и интегрируя, получаем

, (3.3.13.)

Опр. 3.3.1. Относительной скоростью называется отношение скорости молекулы к наиболее вероятной скорости: . (3.3.9.)

При выводе основного уравнения молекулярно-кинетической теории газов и распределения Максвелла предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли.

Барометрическая формула, выражающая зависимость давления идеального газа от высоты над поверхностью Земли: , (3.3.10.)

где давление газа на высоте , давление газа на высоте , абсолютная температура воздуха на высоте . Формула справедлива, если температура не меняется с высотой. Т.к. это не имеет места, то барометрическая формула носит приближенный характер.

Если с помощью барометра измерить давления и , то можно определить высоту: . (3.3.11.)

Барометр, специально проградуированный для отсчета высоты над уровнем моря, называется альтиметром и применяется в авиации, при восхождения на горы и т.п.

Распределение Больцмана (распределение концентрации молекул в силовом поле) , (3.3.12.)

где концентрация частиц в точках пространства, в которых потенциальная энергия равна , концентрация частиц в точках пространства, в которых потенциальная энергия принята равной нулю (на высоте ).

Т.е. при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Опр. 3.3.2. Расстояние, которое молекула пролетает за время свободного пробега от одного столкновения до следующего, называется длиной свободного пробега.

Средняя длина свободного пробега молекул газа (3.3.15.)

- характеристика всей совокупности молекул газа при заданных значениях давления и температуры.

Среднее число соударений, испытываемых одной молекулой газа в единицу времени, ,(3.3.16.)

где эффективный диаметр молекул, число молекул газа в единице объема (концентрация молекул), средняя арифметическая скорость молекул.