Р Дано: , , , ешение:

Д ля начального состояния уравнение Менделеева - Клапейрона имеет вид: . Т.к. объем гелия в конечном состоянии будет таким же (ограничен объемом сосуда), то . Т.к. , то из данных уравнений найдем массы: и , получим .

Ответ: .

Пример 3.2.2. Найти массу киломоля смеси 25 г кислорода и 75 г азота.

Р Дано: ешение:

, где масса смеси равна сумме компонент смеси: . Число киломолей смеси равно сумме киломолей отдельных газов: , т.к. , , то

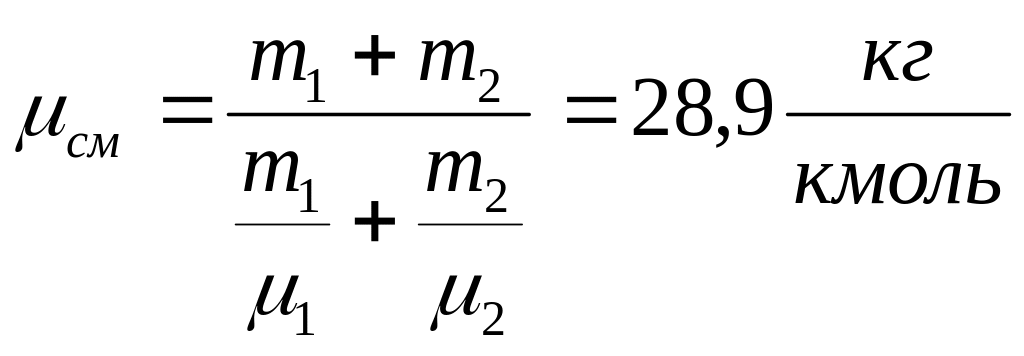
Ответ:

Пример 3.2.3. Определить: 1) сколько молекул содержится в 1 мм³ воды? 2) какова масса молекулы воды? 3) считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр молекул.

1. .Т.к. , , то молекул.

2. Масса одной молекулы: .

3. Если молекулы плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка): , где диаметр молекулы. Если разделить объем одного киломоля вещества на число молекул в киломоле (число Авогадро), то и .

Пример 3.2.4. Какое количество кислорода выпустили из баллона емкостью 10 л, если при этом показания манометра на баллоне изменились от 14 до 17 ат, а температура понизилась от 27⁰С до 7⁰С?

Р Дано: , , , , , ешение:

М асса выпущенного из баллона газа равна разности между начальной массой кислорода в баллоне и его конечной массой . Т.к. условия в баллоне не слишком отличаются от нормальных, газ можно считать идеальным. Для начального и конечного состояний газа в баллоне получим , .

Внимание: чтобы найти давление газа в баллоне, прибавим к показателям манометра величину атмосферного давления, равную 1 ат. Выразим в единицах СИ числовые значения величин: , , , , , , . Получаем .

Ответ: .

Пример 3.2.5. Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.

Р Дано: , , ешение:

С войствами идеального газа могут обладать не только химически однородные газы, но и газовые смеси. Чтобы применить уравнение состояния для газовой смеси, ей необходимо приписать некоторую, хотя и лишенную химического смысла, относительную молекулярную массу. Масса смеси в граммах, численно равная ей, представляет собой молярную массу смеси. Величину выбирают такой, чтобы она удовлетворяла уравнению газового состояния, записанному для смеси: . Рассмотрим каждую из газовых компонент: , , где и парциальные давления каждой компоненты. Для смеси справедлив закон Дальтона: , откуда , а т.к. , то и . Табличные значения , , получаем .

Ответ:

§3.Молекулярно-кинетическая теория газов.

Кинетическая теория газов основана на следующих общих положениях классической статистической физики:

1. в системе частиц выполняются законы сохранения импульса, момента импульса, энергии, электрического заряда (для систем заряженных частиц) и числа частиц (для закрытых систем, не претерпевающих химических и других превращений);

2. все частицы системы считаются «меченными», т.е. предполагается возможность отличать друг от друга тождественные частицы (например, молекулы одного и того же вещества);

3. все физические процессы в системе протекают в пространстве и времени непрерывно (например, энергия молекулы может изменяться под влиянием внешних воздействий на любую величину, т.е. непрерывно);

4. каждая частица системы может иметь совершенно произвольные значения координат (в пределах объема системы) и компонент скорости совершенно независимо от того, каковы значения этих характеристик у других частиц системы.

Важнейшей задачей кинетической теории газов является вычисление давления (макроскопическое проявление теплового движения молекул) идеального газа на основе молекулярно- кинетических представлений.

Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (3.2.6’) (для этого число молекул N возьмём равным числу Авогадро N_А), найдём среднюю кинетическую энергию одной молекулы: , (3.3.1.)

или давление, производимое газом, численно равно средней кинетической энергии поступательного движения молекул в единице объема (или объемной плотности энергии поступательного движения молекул): - (3.3.2.)

основное уравнение кинетической теории газов, где число молекул в единице объема, средняя кинетическая энергия поступательного движения одной молекулы.

Т.о. давление химически однородного идеального газа зависит от массы и концентрации молекул, а также от скоростей их теплового движения.

Т.к. , то (3.3.3.)

Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул (в области температур, далеких от ).

Так как , то средняя квадратичная скорость равна

. (3.3.4.)

Средняя квадратичная скорость является одной из характеристик движения всей совокупности молекул. Она не имеет смысла для одной молекулы или небольшого их числа.

Подставляя значение средней кинетической энергии поступательного движения молекул в основное уравнение молекулярно-кинетической теории газов, получим другую форму уравнения состояния идеального газа: (3.2.6’.)

Основное уравнение кинетической теории газов Клаузиуса: , (3.3.5.)

где . Формулу можно применять для смеси газов.

Средняя кинетическая энергия, приходящаяся на одну степень свободы, . (3.3.6.)

Средняя кинетическая энергия (поступательного и вращательного движений) одной молекулы , (3.3.7.)

где число степеней свободы.

Число степеней свободы есть число независимых координат, определяющих положение молекулы в пространстве. В зависимости от сложности строения молекулы принимает следующие значения (если не учитывать колебаний частей молекул):

для одноатомных газов (молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения; при этом энергию вращательного движения не учитывают);

для двухатомных газов (молекулу двухатомного газа рассматривают как совокупность двух материальных точек, жестко связанных недеформируемой связью. Имеет три степени свободы поступательного движения и две степени вращательного движения. Вращение вокруг третьей оси – проходящей через оба атома - лишено смысла);

для трех- и многоатомных газов (молекулу трехатомного газа рассматривают как совокупность трех материальных точек, жестко связанных недеформируемой связью. Имеет три степени свободы поступательного движения и три степени вращательного движения).