§2.Законы идеальных газов.

Опр.3.2.1. Идеальным называется газ, молекулы которого

1. имеют пренебрежимо малый собственный объем,

2. не взаимодействуют друг с другом на расстоянии,

3. сталкиваются между собой и со стенками сосуда абсолютно упруго.

Т.е. идеальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.

Н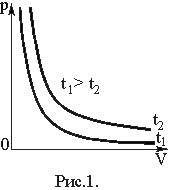 апр., при нормальных условиях (давление и температуре ) водород, гелий, неон, азот, кислород, воздух и др. можно считать с хорошим приближением идеальными.

Для идеальных газов справедливы законы:

а) Закон Бойля-Мариотта. При изотермическом процессе произведение объема данной массы газа (масса неизменна) на давление есть величина постоянная . (3.2.1.)

Для двух состояний газа закон записывается в виде ,(3.2.1’.)

где и давление и объем газа в начальном состоянии, и давление и объем газа в конечном состоянии.

Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1). Изотермы – гиперболы, расположенные на графике тем выше, чем выше температура процесса. б) Закон Дальтона. Давление меси различных газов равно сумме парциальных давлений газов, составляющих смесь: . (3.2.2.)

в) Закон Гей-Люссака. При изобарическом процессе

. (3.2.3.)

( при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре).

Для двух состояний газа , (3.2.3’.)

где и абсолютная температура и объем газа в начальном состоянии, и абсолютная температура и объем газа в конечном состоянии.

Если температура выражена по шкале Цельсия, то , (3.2.3”.)

где температура по шкале Цельсия, объем газа при температуре , объем газа при температуре , коэффициент объемного расширения газов (для идеальных газов , ).

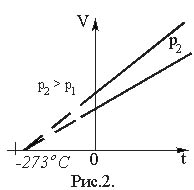
Г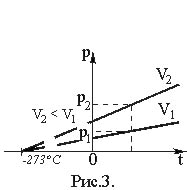 рафически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к –273°С) закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

г) Закон Шарля. При изохорическом процессе . (3.2.4.)

(при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре).

Для двух состояний газа , (3.2.4’.)

где и -абсолютная температура и давление газа в начальном состоянии, и - абсолютная температура и давление газа в конечном состоянии.

Если температура выражена по шкале Цельсия, то ,(3.2.4”.)

где температура по шкале Цельсия, давление газа при температуре , давление газа при температуре , коэффициент объемного расширения газов (для идеальных газов , ).

Графическая зависимость давления от температуры изображается прямой линией – изохорой (рис. 3).

д) Закон Авогадро: при одинаковых давлениях и одинаковых температурах и равных объемах различных идеальных газов содержится одинаковое число молекул; или, что то же самое: при одинаковых давлениях и одинаковых температурах грамм-молекулы различных идеальных газов занимают одинаковые объемы.

Например, при нормальных условиях (t = 0°C и p = 1 атм = 760 мм рт. ст.) грамм-молекулы всех идеальных газов занимают объем 22,414 л. Число молекул, находящихся в 1 см³ идеального газа при нормальных условиях, называется числом Лошмидта; оно равно 2,687*10¹⁹> 1/см³

е) Объединенный газовый закон (уравнение Клапейрона):

- (3.2.5.)

- объединение законов Бойля- Мариотта и Гей – Люссака: для данной массы какого-либо идеального газа произведение давления на объем, деленное на термодинамическую температуру, есть величина постоянная.

Газовая постоянная зависит от химического состава газа и пропорционально его массе. Т.к. ,где удельный объем газа, то уравнение Клапейрона можно переписать: (3.2.5’.)

- уравнение состояния идеального газа.

где р, и Т - давление, молярный объем и абсолютная температура газа, а удельная газовая постоянная, зависящая только от химического состава газа.

Запишем уравнение (3.2.5.) в форме или , (3.2.6.)

где универсальная (молярная) газовая постоянная, численно равная работе, совершаемой 1 молем идеального газа при изобарном нагревании на один градус: . (3.2.7.)

Ее величина найдена экспериментально.

Для произвольной массы газа объем составит и уравнение состояния имеет вид: , (3.2.8.)

где универсальная газовая постоянная, масса киломоля газа, масса газа.

Это уравнение называется уравнением Менделеева - Клапейрона.

Следствия уравнения Менделеева – Клапейрона:

1. плотность газа 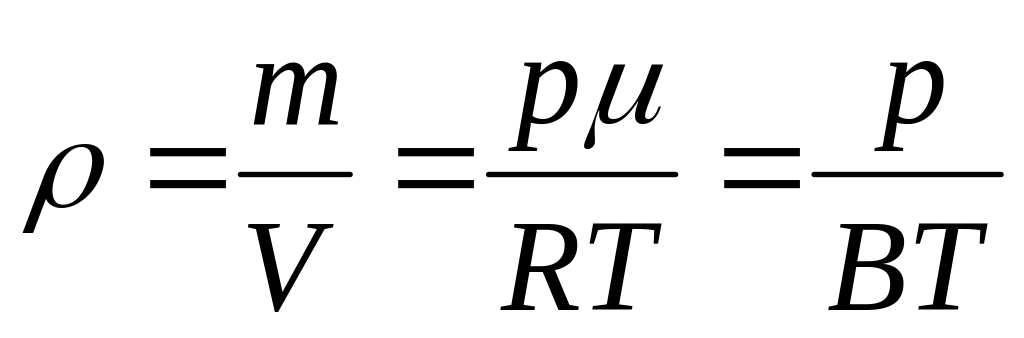. (3.2.9.)

2. число молекул в единице объема 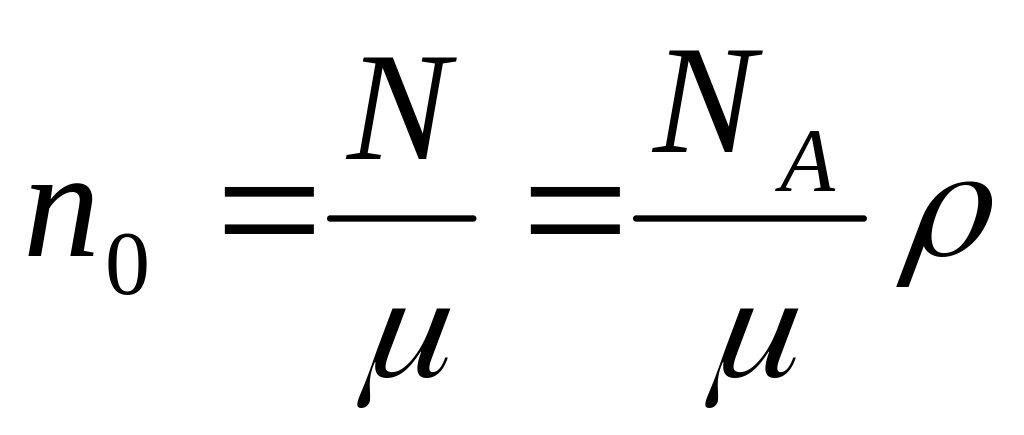. (3.2.10.)

3. концентрация молекул газа . (3.2.11.)

где k - постоянная Больцмана: (3.2.12.)

Уравнение (3.2.6.) можно записать так: (3.2.6’.)

Пример 3.2.1. В баллоне объемом 10 л находится гелий под давлением 10 бар и при температуре 27⁰С. После того, как из баллона было взято 10 г гелия, температура в баллоне понизилась до 17⁰С. Определить давление газа, оставшегося в баллоне.