Решение:

Расширение газа здесь является необратимым процессом. Поэтому нельзя применять формулу . По ней бы мы получили , а по второму закону термодинамики энтропия газа при его необратимом расширении должна увеличиваться. Но т.к. энтропия – функция состояния и ее изменение полностью определяется начальным и конечным состояниями системы, независимо от того процесса, в ходе которого система перешла из начального состояния в конечное. Поэтому представим такой процесс расширения газа, который переводил бы его в то же самое конечное состояние, но являлся бы обратимым процессом и найдем по формуле приращение энтропии в таком обратимом процессе.

Т.к. данный газ изолирован от окружающей среды , то его внутренняя энергия по первому началу термодинамики должна оставаться постоянной. При этом будет постоянной и температура расширения идеального газа во время его расширения, т.е. это изотермическое расширение .

Пример 3.4.9. Исходя из второго начала термодинамики, вывести формулу для к.п.д. цикла Карно.

Решение:

Т.к. цикл Карно – обратимый процесс, то полное изменение энтропии изолированной системы нагреватель - рабочее вещество – холодильник равно нулю: , но полное изменение энтропии складывается из изменения энтропии нагревателя , охладителя и рабочего вещества : . Т.к. рабочее вещество, совершив цикл, вернется в первоначальное состояние, то и . , где знак минус показывает, что нагреватель отдает рабочему телу теплоту, переходя из состояния 1 в состояние 2. Т.к. холодильник получает тепло, то , получим , прибавим к обеим частям равенства по единице . Получаем .

§5.Реальные газы. Жидкости. Реальные газы.

В реальных газах молекулы взаимодействуют друг с другом (силы взаимодействия имеют электромагнитную и квантовую природу). Силы взаимодействия зависят от расстояния между молекулами. Силы межмолекулярного притяжения называют ван-дер-ваальсовыми. Типы сил межмолекулярного притяжения:

ориентационные;

индукционные;

дисперсионные.

Уравнение Ван-дер-Ваальса: для киломоля газа

, (3.5.1.)

для киломолей газа , (3.5.1’.)

где и поправки Ван-дер-Ваальса (рассчитанные на 1 киломоль газа), объем, занимаемый газом, объем одного киломоля газа, число киломолей.

Изотермы реальных газов.

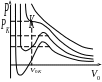
Нанося графически зависимость от из уравнения Ван-дер-Ваальса для различных , мы получим ряд изотерм. Каждая из кривых соответствует определенной температуре : чем выше температура , тем правее и выше лежат на рисунке изотермы. Из рисунка видно, что только при больших температурах изотерма возрастает с уменьшением монотонно, напоминая изотерму, соответствующую закону Бойля – Мариотта. На такой изотерме каждому значению давления соответствует одно значение молярного объема , так же как это имеет место при подчинении газа формуле Менделеева – Клапейрона. При более низких температурах изотермы дают в определенной области давлений и объемов горбы. В этой области, вообще говоря, каждому давлению соответствуют три значения объема . Область горбов на изотермах относится к переходу вещества из газообразного состояния в жидкое и обратно.

Критическая изотерма

Критическая точка

Для анализа состояний неоднородных систем в термодинамике вводится понятие фазы.

Опр.3.5.1. Фазой называется совокупность всех частей системы, обладающих одинаковым химическим составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела.

Типы превращения вещества из одной фазы в другую при изменении внешних условий:

• фазовый переход первого рода – выделяется или поглощается теплота (теплота фазового перехода), скачкообразно меняются плотность, удельный и молярный объемы, концентрация компонентов;

• фазовый переход второго рода – теплота не выделяется и не поглощается, плотность изменяется непрерывно, скачкообразно изменяется молярная теплоемкость, коэффициент теплового расширения, удельная электрическая проводимость, вязкость и т.д.

Соотношения между параметрами критического состояния и постоянными Ван-дер-Ваальса:

• Молярный критический объем газа ,

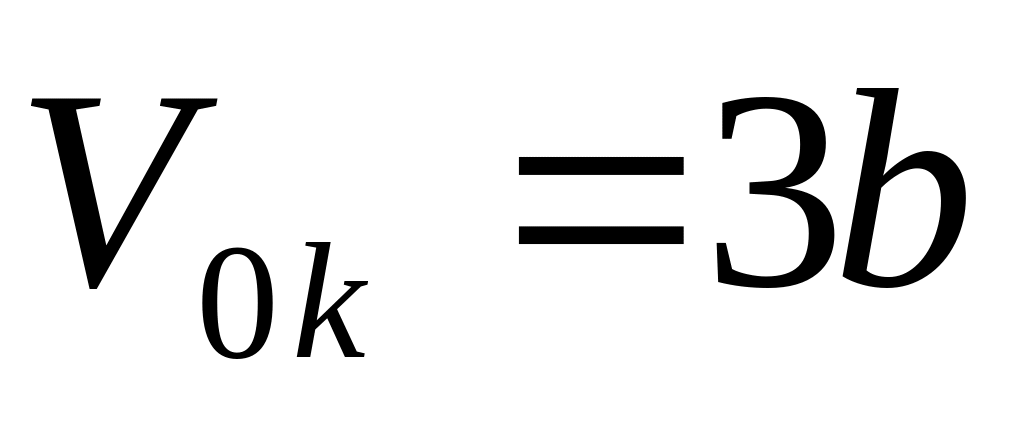• Критическое давление газа ,

• Критическая температура газа .

Коэффициент поверхностного натяжения измеряется силой поверхностного натяжения, действующей на единицу длины любого контура, лежащего на поверхности жидкости: (3.5.2.)

или поверхностной энергией Е, которой обладает каждая единица площади поверхности жидкости: . (3.5.2’.)

Прирост поверхностной энергии связан с увеличением поверхности как . (3.5.3.)

Формула Лапласа: избыточное давление, создаваемое в жидкости вследствие кривизны ее поверхности (поверхностное давление), равно

, (3.5.4.)

где и радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. При этом если поверхность выпуклая, , если вогнутая.

Формула Лапласа в случае сферической поверхности . (3.5.5.)

Высота поднятия жидкости в капилляре радиуса : , (3.5.6.)

где плотность жидкости, ускорение силы тяжести, краевой угол.

Высота поднятия жидкости в капилляре радиуса при полном смачивании: . (3.5.6’.)

Высота подъема жидкости между двумя близкими и параллельным друг другу плоскостями , (3.5.6’’.)

где расстояние меду плоскостями.

Давление насыщающего пара над вогнутой сферической поверхностью жидкости меньше, а над выпуклой - больше, чем над плоской поверхностью, на величину , (3.5.7.)

где радиус сферы, плотности насыщающего пара и жидкости.

Пример 3.5.1. В баллоне емкостью находится 0,3 кг кислорода при температуре 27⁰С. Определить: 1) какую часть объема сосуда составляет собственный объем молекул газа; 2) какую часть давления газа на стенки сосуда составляет внутреннее давление, обусловленное силами притяжения молекул.