Р Дано: , , , , ешение:

И з уравнения Менделеева – Клапейрона определим температуру газа в состоянии 1: , . При изохорическом процессе . При изобарическом процессе . При изохорическом процессе .

Термический (термодинамический) к.п.д. любого цикла определяется формулой , где теплота, полученная газом за один цикл от нагревателя, теплота, отданная газом за один цикл охладителю, теплота, превращаемая в механическую энергию. Термический к.п.д. характеризует степень использования теплоты при превращении ее в механическую энергию, или совершенство цикла, по которому работает тепловая машина.

Теплота, полученная газом при изохорическом процессе (1-2): .

Теплота, полученная газом при изобарическом процессе (2-3): .

Полная теплота, полученная газом от нагревателя: .

Полная теплота, отданная газом охладителю при изохорическом процессе (3-4) и изобарическом процессе (4-5):

, где .

. Разделим числитель и знаменатель дроби на : , где и .

Пример 3.4.5. В цилиндре под поршнем находится водород массой 0,02 кг при температуре 27⁰С. Водород начал расширяться адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершенную газом. Изобразить процесс графически.

Пример 3.4.6. Нагреватель тепловой машины, работающий по обратимому циклу Карно, имеет температуру 200⁰С. Какова температура охладителя, если за счет каждой килокалории тепла, полученной от нагревателя, машина совершает работу 171 ? Потери на трение и теплопередачу не учитываются.

Р Дано: , , , ешение:

Температуру охладителя можно найти, используя выражение для термического к.п.д. машины, работающей по циклу Карно , где абсолютная температура нагревателя, холодильника. Отсюда . Термический к.п.д. тепловой машины есть коэффициент использования теплоты. Он выражает отношение теплоты, которая превращается в механическую работу, к теплоте, которая получена рабочим телом тепловой машины из внешней среды (от нагревателя), т.е. . Впишем числовые значения и получим

Ответ: .

Пример 3.4.7. Найти изменение энтропии при нагревании 100 г воды от 0⁰С до 100⁰С и последующим превращением воды в пар той же температуры.

Решение:

Найдем отдельно изменение энтропии при нагревании воды и изменение энтропии при превращении воды в пар. Полное изменение энтропии выразится суммой . Как известно, изменение энтропии выражается общей формулой .

При бесконечно малом изменении температуры нагреваемого тела затрачивается теплота , где масса тела, его удельная теплоемкость. Т.е. .

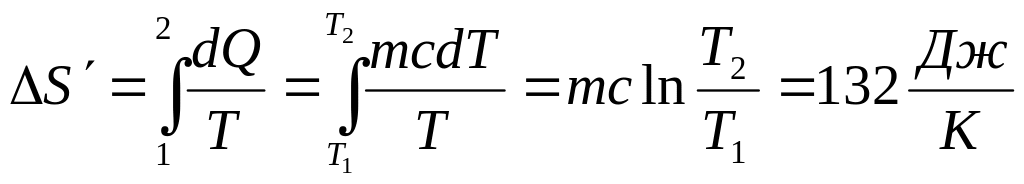Во время превращения воды в пар при той же температуре , где теплота, переданная при превращении нагретой воды в пар той же температуры. Т.к. , где удельная теплота парообразования, то . Полное изменение энтропии при нагревании воды и последующем превращении ее в пар .

Пример 3.4.8. Теплоизолированный сосуд разделен на две равные части перегородкой, в которой имеется закрывающееся отверстие. В одной половине сосуда содержится 10 г водорода. Вторая половина откачана до высокого вакуума. Отверстие в перегородке открывают, и газ заполняет весь объем. Считая газ идеальным, найти приращение его энтропии.