13.Ранг матрицы.Связь ранга с числом независимых строк.

Понятие ранга-одно из фундаментальных понятий лин.алгебры.

Рангом матрицы Am*n наз-ся наивысший порядок,отличных от нуля,миноров этой матрицы.

Свойства ранга:

1)Ранг нулевой матрицы равен 0-- r(0)=0;

2)Ранг не превосходит мини-го из пары чисел m и n:r(A)<=m;n {m;n};

3)Ранг квадр. мат.=n тогда,когда опред-ль /A/не равен 0; r(An)=n.

Теорема:элементарные преоб-я не меняют ранга матрицы.

Элементарные преоб-я:

1.Перестановка строк мат;

2.Прибавление к элем.одной строки соот. элем. другой строки умнож. на некоторое число;

Теорема:

Если строки(столбцы) линейнозависимы,то одно из них явл-ся линейной комбинацией другой.

Теорема о связи ранга мат.с число независимых строк:

Ранг матрицы равен числу её линейнонезависимых независимых строк.

14.Система лин. Ур-й.Элементарные преоб-я над системой.

Матричная запись сист.лин.ур-й.Понятие общего решения.

Система m-лин.ур-й относительно n-ур-й имеет вид:

{a11x1+a12x2+…+a1nxn=b1}

{a21x1+a22x2+…+a2nxn=b2}

…

{am1x1+am2x2+…+amnxn=bm}

Решением сист-наз-ся упоряд.совокупность чисел альфа1,альфа2…альфа n,которая при постановке в сист,каждое ур-е превращает в тождество.

При решении сист. ур-я варианты случая:

1)сист. ур-я имеет 1 решение(совместная);

2)сист.ур-я имеет бесконеч.множ.реш-й(совмест.и неопредел-ая);

3)сист.ур-й не имеет реш-й(несовместная);

Матричная запись:AX=B;

Над сист.ур-я допустимы след.преоб-я:

1)перестановка строк;

2)умнож.обеих частей ур-я на одно и тоже число;

3)вычерк-е нул-вой строки из мат. коэф-тов или ур-я с нул-ми коэф.

4)прибавление к обеим частям одного ур-я соот.частей другого ур-я,умнож. на некоторое число;

В результате преоб-й сист.ур-й,в сист. может появится ур-е вида:

0x1+0x2+…+0xn=0(тривиальное ур-е вычеркивается)

В результате преб-я:

0x1+0x2+…+0xn=и

Тогда ур-е наз-ся противоречивым;сист.,содержащая противоречивое ур-е реш-й не имеет,она не совместна.

15.Реш-е сист.лин.ур-й методом Гаусса.

Пусть дана сист. m лин. ур-й, относительно n:

{a11x1+a12x2+…+a1nxn=b1}

{a21x1+a22x2+…+a2nxn=b2}

(am1x1+am2x2+…+amnxn=bm}

Построим расширенную матрицу:

A р=(a11 a12…a1n/b1)

(a21 a22…a2n/b2)

(am1 am2..amn/bm)

Суть метода Гаусса:

С помощью элем.преоб-й ресшир-я.мат.сист.приводится к треуг-му виду,после привидения начинается обратный ход метода Гаусса.

16. Обратная матрица

Матрица A-1 - обратная для матрицы A, если AA-1=A-1A=I

Для квадратной матрицы A обратная существует тогда и только тогда, когда detA¹0.

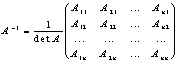
где Aij - алгебраические дополнения элэментов aij матрицы A. Свойства: (A-1)-1=A, (AB)-1=B-1A-1, detA-1=1/detA

В частности:

Решение квадратной системы:

Ax=b

если |A|¹0, то x=A-1b

Матричные уравнения.

XA=B Þ X=BA-1

AX=B Þ X=A-1B

Пусть система линейных алгебраических уравнений задана в матричной форме где матрица A имеет размерность n на n и ее определитель отличен от нуля.

Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы столбца неизвестных переменных .

17. Решение систем линейных уравнений методом Крамера.

Пусть нам требуется решить систему линейных алгебраических уравнений

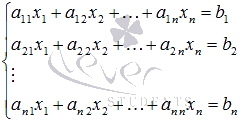
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть,

Пусть - определитель основной матрицы системы, а - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

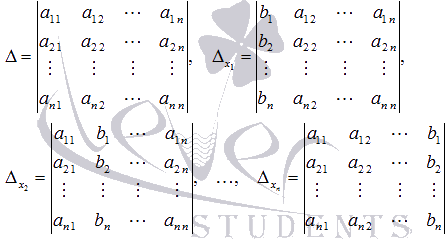
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как .

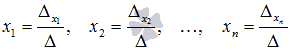18. Теорема Кронекера – Капелли:

для того, чтобы система из p уравнений с n неизвестными была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы.

19. Однородные системы линейных уравнений

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

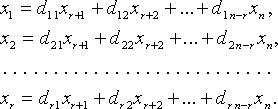
Тогда n - r линейно независимыми вектор-решениями будут:

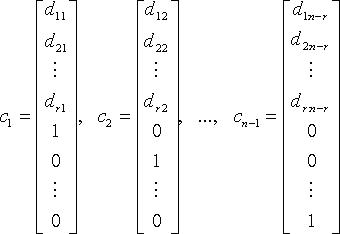
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

21. Модель Леонтьева многоотраслевой экономики.

Эффективное ведение народного хозяйства предалагает наличие

баланса между отдельными отраслями. Каждая отрасль при этом выступает двояко: с одной стороны, как производитель некоторой продукции, а с другой — как потребитель продуктов, вырабатываемых другими отраслями. Для наглядного выражения взаимной связи между отраслями пользуются определенного вида таблицами, называемыми таблицами межотраслевого баланса.

22.Определение линейного оператора. Пусть V и W — линейные пространства, размерности которых

равны соответственно n и m. Мы будем называть оператором А, действующим из V в W, отображение

вида А: V —> W, сопоставляющее каждому элементу х пространства V некоторый элемент у пространства

W. При этом будем использовать обозначение у = А (х) или у = Ах.

Свойства.

1°. λ(АВ) = (λА)В;

2°. (А + В)С = АС + ВС;

3°. А(В + С) = АВ + АС;

4°. (АВ)С = А(ВС).

24. Свойства собственных векторов и собственных значений.

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

1) характеристический многочлен оператора, действующего в R n является многочленом n -й степени

относительно и не зависит от выбора базиса;

2) линейный оператор, действующий в R n имеет не более n различных собственных значений;

3) собственные векторы, отвечающие различным собственным значениям, линейно независимы.

25.Прямоугольные координаты точки на плоскости.

Прямоугольные (декартовы) координаты

точки на плоскости суть снабжённые знаками + или - расстояния

QM = ОР (= х — абсцисса) и РМ = OQ (= у — ордината) точки М от двух взаимно перпендикулярных прямых Ox и Оу (осей координат).

Расстояние между точками на плоскости.

Расстояние между заданными точками равно корню квадратному из суммы квадратов разностей одноимённых координат.

26.Уравнение линии плоскости.

Уравнение линии на плоскости — это уравнение, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Алгебраические линии.

Алгебраической линией порядка n называют уравнение линии, представленное в виде многочлена n степени.

27.Уравнения прямой.

a x + b y = c (a2 + b2 ≠ 0). общее уравнение прямой

y = kx + b уравнение прямой с угловым коэффициентом k

y = y0 + k (x – x0) уравнение прямой с заданным угловым коэффициентом, проходящей через данную точку.

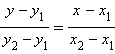прямая, проходящая через две заданные точки.

уравнение прямой в отрезках