Тема 10. Языки запросов

Запрос представляет собой специальным образом описанное требование, определяющее состав производимых над БД операций по выборке, удалению или модификации хранимых данных.

Запрос представляет собой вопрос о данных, хранящихся в таблицах, или инструкцию на отбор записей, подлежащих изменению.

Языки запросов можно разделить на теоретические и практические.

Теоретические языки запросов являются математической основой практических языков запросов.

10.1. Теоретические языки запросов

В реляционных СУБД для выполнения операций над отношениями используются две группы языков, имеющие в качестве своей математической основы теоретические языки запросов, предложенные Э.Коддом:

• реляционная алгебра;

• реляционное исчисление.

Эти языки представляют минимальные возможности реальных языков манипу­лирования данными в соответствии с реляционной моделью и эквивалентны друг другу по своим выразительным возможностям. Существуют не очень сложные правила пре­образования запросов между ними.

В реляционной алгебре операнды и результаты всех действий являются отношени­ями.

Языки реляционной алгебры являются процедурными, так как отношение, явля­ющееся результатом запроса к реляционной БД, вычисляется при выполнении пос­ледовательности реляционных операторов, применяемым к отношениям. (Чтобы получить результат необходимо определить последовательность операторов.)

Операторы состоят из операндов, в роли которых выступают отношения, и реляционных опера­ций.

Результатом реляционной операции является отношение.

Языки исчислений, в отличие от реляционной алгебры, являются непроцедурными (описательными, или декларативными) и позволяют выражать запросы с помощью предиката первого порядка (высказывания в виде функции), которому должны удовлетворять кортежи или домены отношений.

Запрос к БД, выполненный с использованием подобного языка, содержит лишь информацию о желаемом результате.

Для этих языков характерно наличие наборов правил для записи запросов.

В частности, к языкам этой группы относятся QBE и SQL.

10.2. Реляционная алгебра

Напомним, что алгеброй называется множество объектов с заданной на нем со­вокупностью операций, замкнутых относительно этого множества, называемого основным множеством.

Реляционная алгебра как теоретический язык запросов по сравнению с реляционным исчислением более наглядно описывает выполняемые над отношениями действия.

Примером языка запросов, основанного на реляционной алгебре, является ISBL (Information System Base Language — базовый язык информационных систем). Языки запросов, построенные на основе реляционной алгебры, в современных СУБД широкого распространения не получили. Однако знакомство с ней полезно для понима­ния сути реляционных операций, выражаемых другими используемыми языками.

Вариант реляционной алгебры, предложенный Коддом, включает в себя следующие основные операции: объединение, разность (вычитание), пересечение, декартово (прямое) произведение (или произведение), выборка (селекция, ограничение), проекция, деление и соединение. Упрощенное графическое представление этих операций приведено на рис. 10.2.

Операции реляционной алгебры Кодда можно разделить на две группы:

базовые теоретико-множественные

и специальные реляционные.

Первая группа операций включает в себя классические операции теории множеств:

объединение,

разность,

пересечение

и произведение.

Вторая группа представляет собой развитие обычных теоретико-множественных операций в направлении к реальным задачам манипулирования данными, в ее состав входят следующие операции:

проекция,

селекция,

соединение

и деление.

Операции реляционной алгебры могут выполняться над одним отношением (например, проекция) или над двумя отношениями (например, объединение).

В первом случае операция называется унарной, а во втором — бинарной.

При выполнении бинарной операции участвующие в операциях отношения должны быть совместимы по структуре.

Совместимость структур отношений означает совместимость имен атрибутов и типов соответствующих доменов.

Частным случаем совместимости является идентичность (совпадение).

Для устранения конфликтов имен атрибутов в исходных от­ношениях (когда совпадение имен недопустимо), а также для построения произволь­ных имен атрибутов результирующего отношения применяется операция переимено­вания атрибутов.

Структура результирующего отношения по определенным прави­лам наследует свойства структур исходных отношений. В большинстве рассматрива­емых бинарных реляционных операций будем считать, что заголовки исходных отно­шений идентичны, так как в этом случае не возникает проблем с заголовком резуль­тирующего отношения (в общем случае, заголовки могут не совпадать, тогда нужно оговаривать правила формирования заголовка отношения-результата).

По справедливому замечанию Дейта, реляционная алгебра Кодда обладает несколькими недостатками.

Во-первых, восемь перечисленных операций по охвату своих функций, с одной стороны, избыточны, так как минимально необходимый набор составляют пять операций: объединение, вычитание, произведение, проекция и выборка. Три другие операции (пересечение, соединение и деление) можно определить через пять минимально необходимых. Так, например, соединение — это проекция выборки произведения.

Во-вторых, этих восьми операций недостаточно для построения реальной СУБД на принципах реляционной алгебры.

Требуются дополнительные операции, включающие:

переименования атрибутов,

расширения – образования новых вычисляемых атрибутов,

подведения итогов – вычисления итоговых функций,

присвоения,

вставки,

обновления,

удаления,

реляционного сравнения,

построения сложных алгебраических выражений и т. д.

Рассмотрим перечисленные операции более подробно, сначала — операции реляционной алгебры Кодда, а затем — дополнительные операции, введенные Дейтом.

Объединение Разность Пересечение

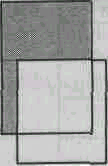
Произведение Выборка (селекция) Проекция

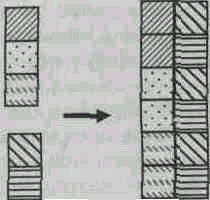
Деление Соединение (естественное)

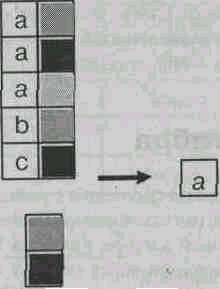
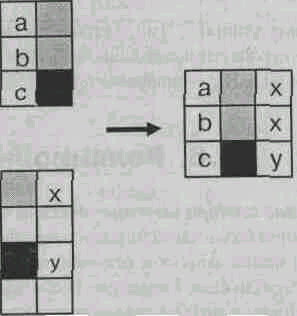
Рис. 10.2. Основные операции реляционной алгебры