1.34. Сужение русла

В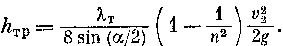 незапное сужение русла (трубы) (рис. 1.69) всегда вызывает меньшую потерю энергии, чем внезапное расширение с таким же соот­ношением площадей. В этом случае потеря обусловлена, во-первых, трением потока при входе в узкую трубу и, во-вторых, потерями на вихреобразование. Последние вызываются тем, что поток не обтекает входной угол, а срывается с него и сужается; кольцевое же прост­ранство вокруг суженной части потока заполняется завихренной жидкостью.

В процессе дальнейшего расширения потока происходит потеря напора, определяемая формулой Борда. Следовательно, пол­ная потеря напора

,

где — коэффициент потерь, обусловленный трением потока при входе в узкую трубу и зависящий от S₁/S₂ и Rе; V_x — скорость потока в суженном месте; — коэффициент сопротивлении внезапного сужения, зависящий от степени сужения.

Для практических расчетов можно пользоваться полуэмпирической формулой И. Е. Идельчика:

,

где n = S₁/S₂ — степень сужения.

Из формулы следует, что в том частном случае, когда можно считать S₂/S₁= 0, т.е. при выходе трубы из резервуара достаточно больших размеров и при отсутствии закругления входного угла, коэффициент сопротивления

.

З

Рис. 1.69. Внезапное сужение трубы

Рис. 1.70. Конфузор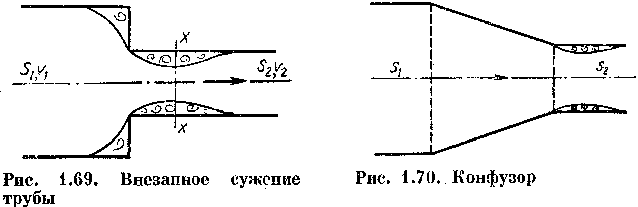

акруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе в трубу.

Постепенное сужение трубы, т. е. коническая сходящаяся труба, называется конфузором (рис. 1.70). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления; так как давление жидкости в начале конфузора выше, чем в конце, причин к возникновению вихреобразовании и срывов потока (как в диффу­зоре) нет. В конфузоре имеются лишь потери на трение. В связи с этим сопротивление конфузора всегда меньше, чем сопротивление такого же диффузора.

Потерю напора на трение в конфузоре можно подсчитать так же, как это делали для диффузора, т. е. сначала выразить потерю для элементарного отрезка, а затем выполнить интегрирование. В резуль­тате получим следующую формулу:

.

Н ебольшое вихреобразование и отрыв по­тока от стенки с одновременным сжатием по­тока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилинд­рической. Для ликвидации вихреобразования и связанных с ним потерь рекомендуется коническую часть плавно сопрягать с цилиндрической или коническую часть заменять криволинейной, плавно переходящей в цилиндрическую (рис. 1.71). При этом можно допустить значительную степень сужения n при небольшой длине вдоль оси и небольших потерях.

К

Рис. 1.71. Сопло

оэффициент сопротивления такого плавного сужения, называе­мого соплом, изменяется примерно в пределах в за­висимости от степени и плавности сужения и Re (большим Re соот­ветствуют малые значения и наоборот).

1.35. Поворот русла

Внезапный поворот трубы, или колено без закругления (рис. 1.72), обычно вызывает значительные потери энергии, так как в нем происходят отрыв потока и вихреобразование, причем эти потери тем больше, чем больше угол δ. Потерю напора рассчитывают до формуле:

.

Коэффициент сопротивления колена круглого сечения воз­растает с увеличением δ очень круто (рис. 1.73) и при δ= 90° дости­гает единицы.

Постепенный поворот трубы, или закругленное колено (рис. 1.74), называется также отводом. Плавность поворота значительно умень­шает интенсивность вихреобразования, а, следовательно, и сопротив­ление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R/d, и при доста­точно большом его значении срыв потока и связанное с ним вихреобразование устраняется полностью. Коэффициент сопротивления отвода зависит от отношения R/d, угла δ, а также формы попереч­ного сечения трубы.

Д

Рис. 1.72. Колено

Рис. 1.73. Зависимость ξ_кол от угла δ

Рис. 1.74. Закругленное колено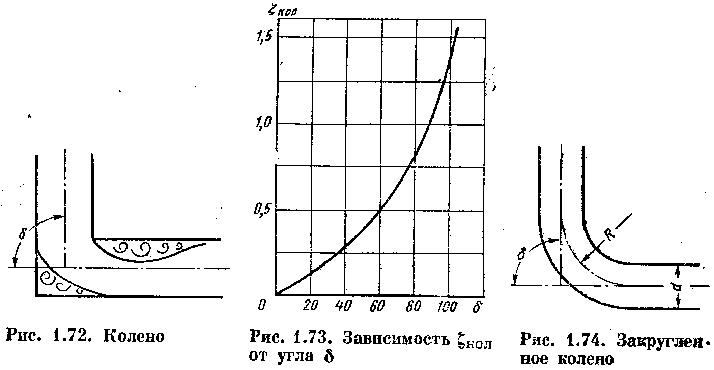

ля отводов круглого сечения с углом δ = 90° и R/d≥1 при турбулентном течении можно пользоваться эмпирической формулой:

.

Для углов δ ≤ 70° коэффициент сопротивления

,

а при δ ≥ 100°

.

Потеря напора, определяемая приведенными коэффициентами учитывает лишь дополнительное сопротивление, обусловленное кривизной русла, поэтому при расчете трубопроводов, содержащих отводы, следует длины этих отводов включать в общую длину трубо­провода, по которой подсчитываете потеря на трение, а затем к этой потере на трение нужно добавить дополнительную потерю от кри­визны, определяемую коэффициентом .

1.36. Местные сопротивления при ламинарном течении

Изложенное в предыдущих параграфах данной главы относилось к местным гидравлическим потерям при турбулентном режиме тече­ния в трубопроводе. При ламинарном режиме, во-первых, местные сопротивления обычно играют малую роль по сравнению с сопротив­лением трения и, во-вторых, закон сопротивления является более сложным и исследован в меньшей степени, чем при турбулентном течении.

Если при турбулентном течении мест­ные потери напора можно считать пропор­циональными скорости (расходу) во второй степени, а коэффициенты потерь опреде­ляются в основном формой местного сопро­тивления и практически не зависят от Re, то при ламинарном течении потерю напора h_м следует рассматривать как сумму

,

г

Рис. 1.75. Схема жиклера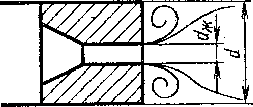

де h_тр — потеря напора, обусловленная непосредственным действием сил тре­ния (вязкости) в данном местном сопротивлении и пропорциональная вязкости жидкости и скорости в первой степени; h_вихр — потеря, связанная с отрывом потока и вихреобразованием в самом местном сопротивлении или за ним и пропорциональная скорости во второй степени.

Так, например, при течении через жиклер (рис. 1.75) слева от плоскости расширения возникает потеря напора на трение, а справа — на вихреобразование.

Учитывая закон сопротивления при ламинарном течения с поправкой на начальный участок, а также формулу , выражение (1) можно представить в виде:

,

где А и В — безразмерные константы, зависящие в основном от формы мест­ного сопротивления.

После деления уравнения (1) на скоростной напор получим общее выражение для коэффициента местного сопротивления при ла­минарном течении в трубопроводе

С

Рис. 1.76 Местное сопротивление

оотношение между первым и вторым членами в формулах (1) и (2) зависит от формы местного сопротивления и числа Re.

В таких местных сопротивлениях, где имеется узкий канал, длина которого значительно превышает его поперечный размер, с плавными очертаниями входа и выхода, как, например, показано на рис. 1.76, а, а числа Re малы, потеря напора определяется в основном трением, и закон сопротивления близок к линейному. Второй член в формулах (1) и (2) в этом случае равен нулю или очень мал по срав­нению с первым.

Если же в местном сопротивлении трение сведено к минимуму, например, благодаря острой кромке (как на рис. 1.76, 6), и имеются отрывы потока и вихреобразование, а числа Re достаточно велики, то потери напора пропорциональ­ны скорости (и расходу) прибли­зительно во второй степени.

При широком диапазоне изме­нения числа Re в одном и том же местном сопротивлении возможен как линейный (при малых Re), так и квадратичный (при больших Re) закон сопротивления, а также переходная между ними область сопротивления при средних Re.

Типичная для такого широко­го диапазона Re зависимость от Re в логарифмических коорди­натах дана на рис. 1.77, где пока­заны результаты испытаний шести сопротивлений. Наклонные прямые соответствуют линейному закону сопротивления (коэффици­ент обратно пропорционален Re), криволинейные участки — переходной области, а горизонталь­ные прямые — квадратичному закону или автомодельности (коэффи­циент не зависит от Re). Такие графики для конкретных мест­ных сопротивлений обычно строят на основе опытных данных.

Иногда вместо двучленной формы выражения местных гидравли­ческих потерь применяют степенной одночлен

.

где k - размерная величина; m — показатель степени, зависящий от формы местного сопротивления и Re к изменяющийся и пределах от 1 до 2. Для местных сопротивлений и Re, при которых закон сопротив­ления близок к линейному, часто применяют выражение местных гидравлических потерь через эквивалентные длины l_фак трубопро­вода, т. е. фактическую длину l_фак трубопровода увеличивают на длину, эквивалентную по своему сопротивлению местным сопротив­лениям.

Таким образом,

и

.

Численные значения эквивалентных длин (отнесенных к диаметру трубопровода) для различных местных сопротивлений обычно на­ходят опытным путем.

Доказанная в п. 1.32 для турбулентного режима теорема о потере напора при внезапном расширении русла при ламинарном режиме неприменима. Дело в том, что в этом случае уже неприемлемы те допущения, которые делались при доказательстве этой теоремы, а именно, предположения о равномерном распределении скоростей в сечениях 1 —1 и 2 — 2, о постоянстве давления по всей пло­щади S2 в сечении 1 — 1 и о равенстве нулю касательных напря­жений.

Как показывают новые экспериментальные исследования, коэффициент потерь для внезапного расширения при очень малых Re (Re < 9) слабо зависит от соотношения площадей и в основном опре­деляется числом Re по формуле вида . Это значит, что те­чение является безотрывным, и потеря на расширение пропорциональна скорости в первой степени. При 9 < Re < 3500 коэффициент потерь зависит как от числа Re, так и от отношения площадей. При Re > 3500 можно считать вполне справедливой теорему Борда, т. е. формулу (число Re определяется по диаметру и скорости до расширения).

Когда по трубе подводится жидкость со скоростью V₁ к резер­вуару больших размеров, где V₂=0, то можно считать, что теряется вся удельная кинетическая энергия жидкости, которая для стабили­зированного ламинарного потока и круглой трубе равна

.

Е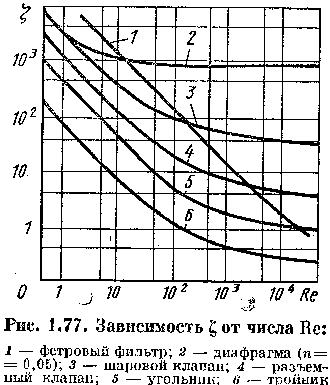 сли же поток не является стабилизированным (длина трубы l < l_нач то коэффициент α_л следует определять по графику, дан­ному на рис. 1.46.

Рис. 1.77. Зависимость ξ от числа Re:

1 – фетровый фильтр; 2 – диафрагма (n=0,05); 3 – шаровой клапан; 4 – разъем- ный клапан; 5 – угольник; 6 - тройник