Прямолинейное равноускоренное движение сосуда с жидкостью.

Ранее было рассмотрено в основном равновесие жидкости под действием лишь одной массовой силы — ее веса. Этот случай имеет место тогда, когда жидкость покоится в сосуде, неподвижном отно­сительно Земли, а также в сосуде, движущемся равномерно и прямо­линейно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Р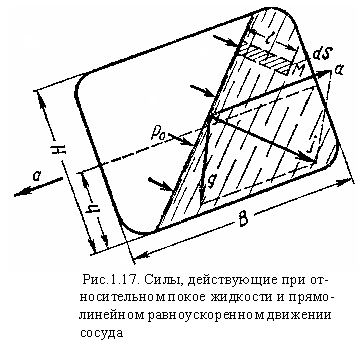 ассмотрим два характер­ных случая относительного по­коя жидкости: в сосуде, дви­жущемся прямолинейно и рав­ноускоренно и в сосуде, вра­щающемся вокруг вертикальной оси с постоянной угловой ско­ростью.

Пусть сосуд с жидкостью движется прямолинейно с постоянным ускорением a. В этом случае результирующую массо­вую силу, действующую на жид­кость, найдем как сумму векто­ров силы инерции, направленной в сторону, обратную ускорению а и силы тяжести {рис, 1.17). Обозначив вектор равнодействующей массовой силы, отнесенной к единице массы, через j, получим:

,

где а и g — векторы единичных сил инерции и тяжести.

Уравнение, позволяющее находить давление в любой точке рас­сматриваемого объема жидкости, можно получить аналогично ,так же как Ур-е гидростатики. Возьмем, например, около точки М пло­щадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический объем с образующей, нормальной к свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид:

,

Где - полная массовая сила, дей­ствующая на выделенный объем жидкости.

l — расстояние от точки M до свободной поверхности

После сокращения на dS получим:

(1.33)

a=0и соответственно j = g, формула (1.33) превращается в основное уравнение гидростатики (1.20).

Равномерное вращение сосуда с жидкостью

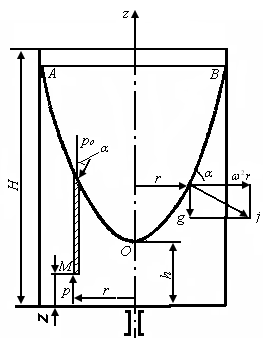
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью ω вокруг его верти­кальной оси. Жидкость постепенно приобретет ту же угловую ско­рость, что и сосуд, а свободная поверхность ее видоизменится; в цент­ральной части уровень жидкости понизится, у стенок — повысится. На жидкость в этом случае будут действовать две массовые силы — сила тяжести и центробежная сила. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сала нормальна к свободной поверхности жидко­сти, поэтому наклон этой поверхности с увеличением радиуса возрастает.