Г л а в а 2. Гидростатика

1.4. Гидростатическое давление и его свойство

Гидростатикой называется раздел гидравлики, в котором рас­сматриваются законы равновесия жидкости и их практические при­ложения.

Как следует из гл. 1, жидкости практически не способны сопро­тивляться растяжению, а в неподвижных жидкостях не действуют касательные силы. Поэтому на неподвижную жидкость из поверх­ностных сил могут действовать только силы давления; причем на внешней поверхности рассматриваемого объема жидкости силы давле­ния всегда направлены по нормали внутрь объема жидкости и, сле­довательно, являются сжимающими. Под внешней поверхностью жидкости понимают не только поверхность раздела жидкости с газо­образной средой или твердыми стенками, но и поверхность объема, мысленно выделяемого из общего объема жидкости.

Таким образом, в неподвижной жидкости возможен лишь один вид напряжения — напряжение сжатия, т. е. гидростатическое дав­ление.

Введем понятие о гидростатическом давлении. Рассмотрим объем жидкости, находящейся в равновесии. Разделим его плоскостью ВС на две произвольные части Iи II Первую часть отбросим (рис. 3.2), а для сохранения равновесия части II суммарное воздействие на нее отброшенной части I заменим силой Р. Тогда напряжение будет называться средним гидростатическим давлением, действую­щим на площадку , а предел отношения

— гидростатическим давлением в данной точке А, т. е. гидростати­ческое давление есть напряжение, возникающее в жидкости, нахо­дящейся в равновесии. Единица измерения давления в системе СИ: Па = Н/м².

Р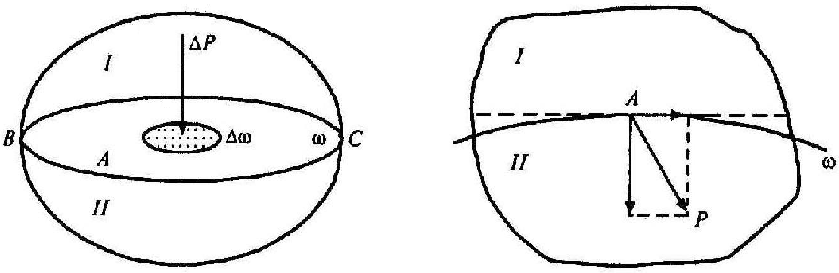 ассмотрим основное свойство гидростатического давления: в лю-­ бой точке жидкости гидростатическое давление не зависит от ориен-­ тировки площадки, на которую оно действует, т. е. от углов ее на-­ клона по отношению к координатным осям.

Для доказательства этого свойства выделим в неподвижной жид­кости элементарный объем в форме тетраэдра е ребрами, параллель­ными координатным осям и соответственно равными dx, dy и dz (рис. 1.6). Пусть внутри выделенного, объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z. Обозначим через р_х гидростатическое давление, действующее на грань, нормальную к оси Ох, через p — давление на грань, нор­мальную к оси Оу, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через р , а площадь этой грани — через dS.

Составим уравнение:

(1)

Масса жидкости в тетраэдре равна произведению ее объема на плотность.

Уравнение равновесия тетраэдра запишем в виде:

(2)

Разделив это уравнение па площадь dydz/2, которая равна площади проекций наклонной грани dS на плоскость yOz, т. е. dydz/2 == dScos(n,x), получим:

(3)

П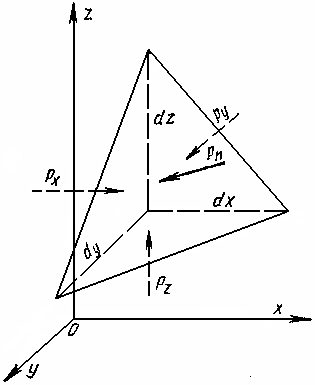 ри стремлении размеров тетраэдра к нулю последний член уравнения содержащий множитель dx, также стремится к нулю, а давления р_х и р_п остаются

вели­чинами конечными. Следователь­но, в пределе получим Рх — Рп = 0 или р_х = р_п.

Аналогично составляя уравне­ния равновесия вдоль осей Оу и Oz, находим

или

Так как размеры тетраэдра dx, dy и dz взяты произвольно, то и наклон площадки dS произволен и, следовательно, дав­ление в этой точке по всем на­правлениям будет одинаково.

Рис.1.6.Сема для доказательства свойства

гидростатического давления

Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же реальной жидкости возникают касательные напряжения, давление в реальной жидкости указанным свойством, не обладает.