Оптимизация Балансировка
Внимательный
читатель, услышав слово «дерево»
неизбежно вспомнил бы и два других —
«логарифм» и «балансировка». И, как
всегда, чтобы достичь заветной
логарифмической асимптотики придется
все таки балансировать наше дерево.
Действительно, при нынешнем способе
слияния строк внутренняя структура
дерева будет похожа скорее на «лестницу»,
например такую, как на рисунке
ниже:
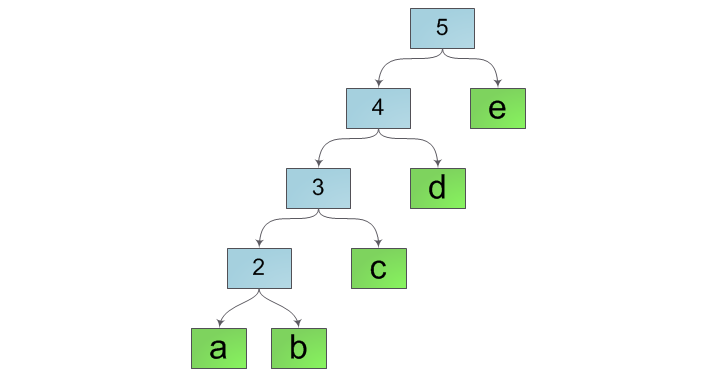Чтобы
этого избежать, будем при каждом
объединении строк проверять
сбалансированность результата и при
необходимости пересобирать все дерево,
балансируя его. Хорошее условие
сбалансированности — длина строки
должна быть не меньше (h+2) — го числа
Фибоначчи. Обоснование этого условия
а также пара дополнительных модификаций
операции склейки были даны Боэмом,
Аткинсоном и Плассом в их работе Ropes:
an Alternative to Strings
Прямое объединение малых строк
Хранение в памяти узлов дерева вовсе не бесплатно. Если к строке прибавлять по одному символу то мы потратим на хранение информации об узлах дерева на порядок больше памяти, чем на сами символы строки. Во избежание таких ситуаций, а также для уменьшения высоты дерева целесообразно склеивать строки меньше некоторой длины (например, 32) «классическим» способом. Это сильно сэкономит память а также почти не отразится на производительности в целом.
Кэширование последней позиции
В подавляющем числе случаев мы перебираем символы строки последовательно. В нашем случае, если мы запрашиваем символы по индексам i и i+1 очень велика вероятность того что физически они находятся в одном и том же листе дерева. Это значит что при поиске этих символов мы будем повторять один и тот же путь от корня дерева до листа. Очевидное решение этой проблемы — кэширование. Для этого при поиске очередного символа запомним лист в котором он находится и диапазон индексов, которые этот лист в себе содержит. После, при поиске очередного символа сперва будем проверять, лежит ли наш индекс в запомненном диапазоне и, если это так, будем искать его непосредственно в запомненном листе. Можно даже пойти дальше, запоминая не одну последнюю позицию а несколько, например, в циклическом списке. Вкупе с предыдущей оптимизацией такая техника позволит нам улучшить асимптотику индексации с O(ln(n)) практически до О(1).
ЗАКЛЮЧЕНИЕ
В результате выполнения работы разработан и исследован алгоритм Rope на основе деревья поиска (Search trees).
Осуществлено моделирование разработанного алгоритма. Показано, что он может создавать корень дерева для быстрых строк, и добавлять по индексу подстроки. Так же были реализованы выводы всей строки и длины подстрок входящие в нее.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Хорошевский В.Г. Архитектура вычислительных систем. – М.: МГТУ им. Н.Э. Баумана, 2008. – 520 с.
Ropes: an Alternative to Strings SOFTWARE—PRACTICE AND EXPERIENCE, VOL. 25(12), 1315–1330 (DECEMBER 1995)
http://habrahabr.ru 21.12.2012
еn.wikipedia.org/wiki/Rope_(data_structure) 13.12.2012
1 Исходный текст программы
/* * ropestring_create + * ropestring_add_index + * ropestring_lenght_substrings + */ if (node != NULL) { node->left = NULL; node->right = NULL; node->l = l; node->r = r; node->lenleft = lenleft; node->lenright = lenright; } return node; } struct ropestring *ropestring_add_index(struct ropestring *tree, int index, char *path) { if (index <= tree->lenleft) { tree->lenleft += strlen(path); if (tree->left != NULL) { ropestring_add_index(tree->left, index, path); return; } else { tree->left = ropestring_create(tree->l, &(tree->l)[index], index, tree->lenleft - index - strlen(path)); tree->l = NULL; tree = tree->left; tree->left = ropestring_create(tree->l, path, tree->lenleft, strlen(path)); tree->lenleft += strlen(path); } } else if (index <= (tree->lenleft + tree->lenright)) { #include <stdio.h> #include <stdlib.h> #include <string.h> struct ropestring { int lenleft; int lenright; char *l; char *r; struct ropestring *left; struct ropestring *right; }; struct ropestring *ropestring_create(char *l, char *r, int lenleft, int lenright) { struct ropestring *node; node = malloc(sizeof(*node)); tree->lenright += strlen(path); if (tree->right != NULL) { ropestring_add_index(tree->right, index, path); return; } else { index -= tree->lenleft; tree->right = ropestring_create(tree->r, &(tree->r)[index], index, tree->lenright - index - strlen(path)); tree->r = NULL; tree = tree->right; tree->left = ropestring_create(tree->l, path, tree->lenleft, strlen(path)); tree->lenleft += strlen(path); } }else if (index > (tree->lenleft + tree->lenright)) { tree->lenright += strlen(path); if (tree->right != NULL) { ropestring_add_index(tree->right, index, path); return; } else { index -= tree->lenleft; tree->right = ropestring_create(tree->r, path, tree->lenright - strlen(path), strlen(path)); tree->r = NULL; } } } void ropestring_print(struct ropestring *tree) { int i; if (tree == NULL) return; if (tree->left != NULL){ ropestring_print(tree->left); } else { for (i = 0; i < tree->lenleft; i++) printf("%c", tree->l[i]); } if (tree->right != NULL) ropestring_print(tree->right); else { for (i = 0; i < tree->lenright; i++) printf("%c", tree->r[i]); } return; } void ropestring_lenght_substrings(struct ropestring *tree) { if (tree == NULL) return; if (tree->left != NULL) ropestring_lenght_substrings(tree->left); else { if (tree->lenleft!=0) printf ("(%d)",tree->lenleft); } if (tree->right != NULL) ropestring_lenght_substrings(tree->right); else { if (tree->lenright != 0) printf("(%d)", tree->lenright); } return; } int main() { struct ropestring *tree = NULL; tree = ropestring_create ("Ropestring", "leftright", strlen("Ropestring"), strlen("leftright")); ropestring_add_index(tree, 4, "_+_"); ropestring_add_index(tree, 0, "<<<"); ropestring_add_index(tree, 16, "==="); ropestring_add_index(tree, 23, "_+_"); ropestring_add_index(tree, 31, ">>>"); ropestring_print(tree); printf ("\n"); ropestring_lenght_substrings (tree) ; printf ("\n"); return(0); }