Последовательное кодирование (при наличии цап)
АЦП данного типа в виду своей дешевизны широко распространены в бытовой технике. По своей внутренней структуре эти АЦП можно условно разделить на два типа: с применением ЦАП и без них. К первому относятся АЦП последовательного счета и последовательных приближений. Алгоритм их работы во многом аналогичен и различается, главным образом, элементной базой.
Рассмотрим сначала основную идею метода. Она очень напоминает детскую игру “угадай число”. В этой игре с двумя участниками один загадывает число в заранее оговоренном интервале, а второй отгадывает это число. В ходе игры отгадывающий предлагает возможный варианты, а загадавший (ответ) каждый раз сообщает о соотношении предложенного варианта с задуманным им числом (больше или меньше). Если целью этой игры является отгадывание числа за минимальное количество обращений к задумавшему число, то целью самых простых АЦП является “отгадывание” амплитуды аналогового сигнала на его входе путем простого перебора всех возможных состояний (цифровых кодов), устанавливаемых на входе ЦАП, начиная с нулевого кода, до того кода, когда напряжение на выходе ЦАП не превысит (сравняется) с входным аналоговым (измеряемым) сигналом. Операцию сравнения входного напряжения и напряжения с выхода внутреннего ЦАП производится с помощью внутреннего компаратора, который обязательно входит во все АЦП на основе метода последовательного кодирования (МПК).
Описанная выше разновидность МПК называется методом последовательного счета. Более прогрессивная разновидность МПК - метод последовательных приближений или метод поразрядного взвешивания. Он начал применяться несколько позднее первой, т. к. для этого надо было разработать специальный регистр. Этот регистр получил название регистр последовательных приближений (РПП). Английское название successive approximation register (SAR). Идея метода совпадает с идеей метода половинного деления, часто используемого при отгадывании числа в игре “угадай число”. Сначала полный диапазон разбивается на две равные части (интервал поиска сокращается в два раза), затем выбирается тот интервал, в котором находится задуманное число. Полученный интервал снова делится пополам (интервал поиска сокращается уже в четыре раза по отношению к полной шкале). Процедура повторяется многократно, до тех пор, пока не будет найден ответ. Говоря языком теории информации, на каждом шаге (приближении) энтропия измеряемой величины уменьшается в два раза.
Хотя в математике применяют другие, более быстросходящиеся методы, но применение их в АЦП вряд ли оправдано, т. к. их преимущество перед методом половинного деления в скорости было бы заметно лишь для АЦП с очень большим числом разрядов. Для АЦП с небольшим числом разрядов применение этих методов приведет к не оправданному усложнению аппаратного содержания АЦП, т. к. выполнение операции деления на два в двоичном счислении просто заменяется сдвигом на один разряд вправо. Деление на число отличное от двух предполагает выполнение длинной цепочки операций сдвига и сложения .
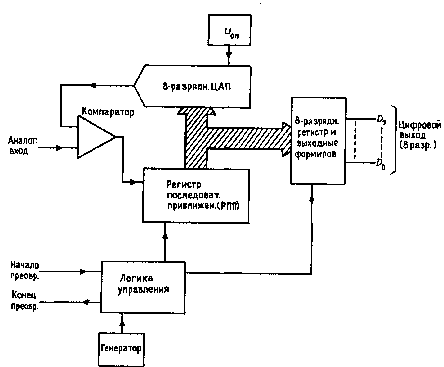
Рис.4.4. Блок-схема АЦП последовательных приближений |