Понятие обратной функции

    Если функция задана уравнением вида f (x, y) = 0, не разрешенным относительно у, то она при некоторых условиях называется неявной функцией аргумента x.    Пусть задана некоторая функция у = f(х), которая каждому элементу из множества D (f) ставится в соответствие один элемент из множества Е ( f ). Если обратное соответствие есть тоже функция, то есть, каждому значению у   E( f ) соответствует единственное значение х   D ( f ), то ее называют обратной функцией по отношению к функции f (х).    В этом случае соотношение у = f (х) определяет х как неявную функцию от у. Если это соотношение разрешимо относительно х, то получим явное выражение обратной функции: х = g (у).   Если функция g является обратной по отношению к функции f, то и функция f является обратной по отношению к функции g, т. е. эти две функции - взаимно-обратные.   Одна и та же кривая у = f (х) представляет собой график функции у = f (х) и график обратной функции х = g (у) (если она существует), но в последнем случае значения аргумента рассматриваются на оси Оу, а значения функции - на оси Ох.   Если придерживаться стандартных обозначений и независимую переменную обозначать через х, а функцию − через у, то функция, обратная по отношению к у = f(х), запишется в виде у = g (х). В этом случае график функции у = g (х) симметричен графику функции у = f (х) относительно прямой у = х − биссектрисы I и III координатных углов.   Для взаимно - обратных функций имеют место следующие соотношения

D ( f ) = E ( g ), E ( f )= D (g),

т. е. область определения данной функции совпадает с множеством значений обратной функции, и наоборот.

Классификация элементарных функций.

Для чего нужно классифицировать элементарные функции? Ответ очень прост: каждому классу функций соответствует определенный набор свойств. Некоторые функции бесконечное число раз дифференцируемы на каком-либо промежутке, некоторые непрерывны, другие ортогональны с весом и т.д. и т.п. Согласитесь, когда все книги разложены по-полочкам по определенным тематикам, достаточно просто найти нужную...  Определение элементарной функции. Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий (сложение, вычитание, умножение, деление) и образования сложных функций, называютсяэлементарными функциями . Примером может являться функция 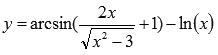 Очень удобно классификацию элементарных функций представить в виде таблицы.

• Элементарные функции

• Трансцендентные

• Алгебраические

• Иррациональные

• Рациональные

• Целые рациональные

• Дробные рациональные

Элементарные функции подразделяются на алгебраические и трансцендентные. Определение алгебраических функций. Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня. Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты. Например, функция 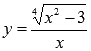  является алгебраической. Определение трансцендентной функции. Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций). К примеру, 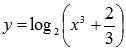  - трансцендентная функция. Алгебраические функции подразделяются на рациональные и иррациональные . Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов). Пример целой рациональной функции:  . Пример дробно-рациональной функции:  . ПРИМЕЧАНИЕ: Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, 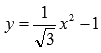  - целая рациональная функция, а не иррациональная. Определение иррациональной функции. Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня). Примером может являться функция  . ПРИМЕЧАНИЕ: Если вид функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция. К примеру,   - не иррациональная функция, а рациональная, так как  ;  - не трансцендентная функция, а рациональная алгебраическая, так как  .