Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy= f (x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f (x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dx) = d2y = f (x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1-го порядка:

dⁿy = d(dⁿ–1 y) = f(n)(x)dx(n).

Дифференциал и его связь с производной

Дифференциал функции. Геометрический смысл дифференциала.

 

Дифференциал функции - это произведение производной  f ’( x₀ ) и приращения аргумента    :

df = f ’( x₀ ) ·  .

Геометрический смысл дифференциала ясен из рис.2:  здесь  df = CD

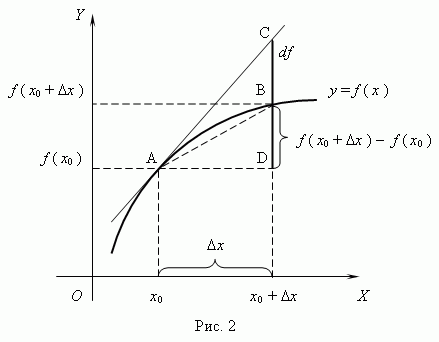
I Дифференциальное исчисление функции одной переменной Понятие производной

Рассмотрим задачу, которая приводит к понятию производной. Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t₀. За период от t₀ до t₀+ t количество продукции изменится от u(t₀) до u₀+ u = u(t₀+ t). Тогда средняя производительность труда за этот период z =  u/ t, поэтому производительность труда в момент t₀

z = lim_ t 0 u/ t.

Определение 1 (производная). Производной функции y = f(x) в фиксированной точке x называется предел

lim_ x 0 y/ x

при условии существования этого предела.

Производная обозначается следующим образом f'(x) или y'.

Пример 1. Вычислить производную функции y = sin x. Найдем приращение функции:

 y = sin(x+ x)-sin x = 2sin( x/2) cos (x+ x/2).

По определению производной

(sin x)' = lim_ x 0 y/ x = lim_ x 0(cos (x+ x/2)(sin  x/2)/( x/2)) = =cos x,

так как

lim_ x 0cos (x+ x/2) = cos x.

Таким образом,

(sin x)' = cos x.

Определение 2. Правой (левой) производной называется правый (левый) предел

lim_{ x 0 + 0} y/ x

lim_{ x 0 - 0} y/ x ,

если эти пределы существуют.

Для обозначения правой (левой) производной используют символ: f'(x+0) f'(x-0). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).

Пример 2. Доказать, что f(x) = 3|x|+1 не имеет производной в точке x = 0. Составим  y = 3(0+ x)+1-1=3 x при  x>0. При  x<0  y = -3(0+ x)+1-1=-3 x, значит,

lim_{ x 0-0} y/ x =-3, lim_{ x 0+0} y/ x = 3.

Поэтому данная функция не имеет производной в точке x = 0.

Геометрический смысл производной

Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение  x 0, причем x+ x  (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+ x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+ x,f(x+ x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через  ( x).

Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при  x 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.

Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim_ x 0 ( x) =  ₀, который равен углу, образованному касательной с положительным направлением оси OX.

Справедливо утверждение:

Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке  M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).

Из этого утверждения вытекает геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции.

Тогда уравнение касательной к кривой f(x) в точке x₀ имеет вид

y = f(x0)+f'(x0)(x-x0)

Пример 3. Составить уравнение касательной к кривой y = 2x²-x+5 при x = -0,5.

Решение. Найдем производную в точке x = -0,5

y' = 4x-1, y'(-0,5) = -3.

Уравнение касательной имеет вид:

y = 6-3(x+0,5) или y = -3x+4,5.

h4>Дифференцируемость функции Пусть функция определена на интервале (a,b).

Определение 4 (дифференцируемость в точке). Функция f(x) называется дифференцируемой в точке x, если приращение  y этой функции в точке x представимо в виде

 y =A x + ( x)  x,

(1)

где A - некоторое число, не зависящее от  x, а lim_ x 0  ( x ) = 0.

В дальнейшем будем считать, что (0) = 0. В этом случае функция (x) будет непрерывной в точке  x = 0. Равенство 1 можно переписать иначе, так как функции  ( x),  x - бесконечно малые в точке  x = 0 и их произведение тоже бесконечно малая функция, поэтому

 y =A x +o( x).

(2)

Справедлива теорема

Теорема 1. Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на  x 0 получим

 y/ x = A+( x).

Переходя к пределу в последнем выражении при  x 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

lim_ x 0 y/ x = f'(x).

Обозначим ( x) =  y/  x-f'(x). Отсюда вытекает представление (1).

Пример 4. Доказать, что функция |x| не дифференцируема в точке x = 0.

Решение. Найдем приращение функции в точке x = 0 :

 y = | x|

Поэтому

lim_{ x -0} y/ x = -1, lim_{ x +0} y/ x = 1,

следовательно, функция |x| в точке x = 0 не дифференцируема.

Следующая теорема выражает связь между непрерывностью и дифференцируемостью.

Теорема 2 (дифференцируемость и непрерывность). Если  функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_ x 0 y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называетсякусочно гладкой.