Непрерывность функций на интервале

  Будем говорить, что функция f (x) непрерывна в интервале (а, b), если она непрерывна в каждой точке этого интервала; непрерывна на отрезке [а, b], если она непрерывна в интервале (а, b) и непрерывна в точке x = а справа, а в точке x = b слева, т. е.

 и 

Непрерывность рациональных функций

  Простейшим примером функции, непрерывной в любой точке х₀ числовой прямой, может служить постоянная функция f (x) = c.   Действительно, в этом случае

т. е. постоянная функция непрерывна в каждой точке числовой прямой.    Функция f (x) = x непрерывна также в каждой точке х₀ числовой прямой, так как предел функции в точке х₀ равен ее значению в этой точке:

  Из сказанного следует, что в любой точке х₀ функции х² = х ·x, х³ = х²· x, …, хⁿ = x^n-1·x (n - натуральное число) непрерывны.   Функция f (x) = xⁿ называется степенной, а функция вида

P_n = C₀ xⁿ + C₁ x^{n - 1} + C₂ x^{n - 2} + … + C_{n - 1} x + C_n

называется алгебраическим многочленом, где n ≥ 0 — целое число; С₀, С₁, С₂, …, С_n — любые числа. Каждое из слагаемых слагаемых в выражении многочлена

P_n = C₀ xⁿ + C₁ x^{n - 1} + C₂ x^{n - 2} + … + C_{n - 1} x + C_n

является непрерывным в любой точке х.   Дробно рациональная функция

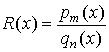
где p_m(х) и q_n(х) — алгебраические многочлены, непрерывна во всех таких точках х числовой оси, в которых ее знаменатель не равен нулю.

Непрерывность тригонометрических функций

  Рассмотрим тригонометрические функции sin х, cos х, tg х, ctg х, sec x, cosec х.   Функция sin х непрерывна в любой точке числовой прямой.    Рассмотрим разность

,

если | x − x₀ | мало, то | sin x − sin x₀ | тоже достаточно мало:

(   ε > 0 ) (   δ = δ (ε, x₀) > 0 ) (  | x - x₀ | < δ ) : | sin x − sin x₀ | < ε

Таким образом, функция sin x непрерывна в любой точке числовой оси.    Непрерывность функции cos x в любой точке числовой оси доказывается аналогично. Рассмотрим разность

если | x − x₀ | мало, то |cos x − cos x₀| тоже достаточно мало:

(   ε > 0 ) (   δ = δ (ε, x₀) > 0 ) (  | x - x₀ | < δ ) : | cos x - cos x₀ | < ε

  Из непрерывности функций sin x и cos x следует непрерывность функций tg x и sec x во всех точках, где cos x ≠ 0, т.е. во всех точках, кроме х = /2 + · k ( k   Z), и функций ctg x и cosec x во всех точках, кроме х = · k (k = 0, ±1, ±2,… ).

Непрерывность функции f (x) = |x|

  Функция f (x) = | x |. график которой изображен на рис. 5.14 определена и непрерывна во всех табличках числовой прямой.    Действительно, в точках полупрямой (0; + ∞) функция f(x) = x непрерывна. В точках полупрямой (- ∞; 0) функция f( x ) = − x также непрерывна. Чтобы установить непрерывность функции в точке x = 0 вычислим односторонние пределы функции в этой точке

  

Пределы функции в точке х = 0 слева и справа совпадают и равны значению функции в этой точке. Отсюда следует, что функция непрерывна в точке х = 0 и, следовательно, непрерывна во всех точках числовой прямой.

Непрерывность показательной функции

   Докажем что  .   Доказательство. Так как для любого аргумента можно найти два последовательных натуральных числа, что будут выполнены условия n < x < n + 1. По свойству неравенств имеем

.

При а > 1 показательная функция является монотонно возрастающей, поэтому

.

Так как  , то по теореме о пределе промежуточной функции справедливо соотношение

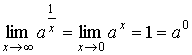
Далее имеем,  , что и требовалось доказать.