- •Область определения функции. Необходимые сведения и примеры нахождения.
- •Основные элементарные функции, их свойства и графики.
- •Степенная функция.
- •Степенная функция с нечетным положительным показателем.
- •Степенная функция с нечетным отрицательным показателем.
- •Степенная функция с четным положительным показателем.
- •Степенная функция с четным отрицательным показателем.
- •Степенная функция с рациональным показателем.
- •Показательная функция.
- •Логарифмическая функция.
- •Тригонометрические функции, их свойства и графики.
- •Обратные тригонометрические функции, их свойства и графики.
- •Сложная функция
- •Понятие обратной функции
- •Классификация элементарных функций.
- •Определение предела последовательности
- •Бесконечно - малые последовательности
- •Свойства сходящихся последовательностей
- •Пределы функций. Примеры решений
- •1. Понять, что такое предел. 2. Научиться решать основные типы пределов.
- •1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
- •2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.Д.
- •Первый замечательный предел
- •Второй замечательный предел
- •Определение непрерывности функции
- •Классификация точек разрыва функции
- •Арифметические действия над непрерывными функциями
- •Непрерывность функций на интервале
- •Непрерывность рациональных функций
- •Непрерывность тригонометрических функций
- •Непрерывность показательной функции
- •Производная, основные определения и понятия.
- •Касательные и нормали к кривым
- •Эту теорему легко обобщить на случай большего числа функций одного аргумента:
- •Производная
- •Дифференцируемость функций.
- •Непрерывность функции, имеющей производную. Теорема.
- •Производные различных порядков.
- •Дифференциалы различных порядков.
- •Дифференциал и его связь с производной
- •I Дифференциальное исчисление функции одной переменной Понятие производной
- •Геометрический смысл производной
- •Правила дифференцирования
- •Дифференцирование сложной и обратной функций
- •Производная степенно-показательной функции
- •Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
- •Производные и дифференциалы высших порядков
- •Производная параметрически и неявно заданных функций
- •Основные теоремы дифференциального исчисления
- •Правило Лопиталя
- •Формула Тейлора
- •Выпуклость функции. Точки перегиба
- •Асимптоты графика функции
- •Общая схема исследования функций и построение их графиков
- •Экономический смысл производной
- •Максимизация прибыли
- •Оптимизация налогообложения предприятий
- •Интегральное исчисление функции одной переменной Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Метод подстановки
Область определения функции. Необходимые сведения и примеры нахождения.
Эта
тема очень важна, так как все наши
действия с функциями и выражениями
возможны лишь на области их определения.
С ее нахождения и следует начинать
решение практически любых
задач.
Определение
Областью
определения функции ![]() (выражения f(x) )
называют множество всех значений x ,
для которых функция (выражение) имеет
смысл.
Область определения
функции
обозначается
как
(выражения f(x) )
называют множество всех значений x ,
для которых функция (выражение) имеет
смысл.
Область определения
функции
обозначается
как ![]() или
или ![]() .
Дальнейшее
изложение предполагает знание областей
определения основных
элементарных функций,
знаниеклассификации
элементарных функций ,
а так же умение решать различные виды
неравенств и систем неравенств.
При
нахождении области определения функции
приходится решать различные неравенства
(иррациональные, логарифмические,
тригонометрические и т.п.) и системы
неравенств. Мы не будем подробно
останавливаться на их решении, а иногда
и вовсе будем оставлять без решения,
так как это выходит за рамки данного
раздела.
Что
указывает на наличие ограничений области
определения:
.
Дальнейшее
изложение предполагает знание областей
определения основных
элементарных функций,
знаниеклассификации
элементарных функций ,
а так же умение решать различные виды
неравенств и систем неравенств.
При
нахождении области определения функции
приходится решать различные неравенства
(иррациональные, логарифмические,
тригонометрические и т.п.) и системы
неравенств. Мы не будем подробно
останавливаться на их решении, а иногда
и вовсе будем оставлять без решения,
так как это выходит за рамки данного
раздела.
Что
указывает на наличие ограничений области
определения:
присутствие корней четной степени вида
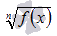 ,
где n -
четное, например,
,
где n -
четное, например, 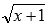 (наличие
степенной функции с дробным показателем,
знаменатель которого есть четное число,
например,
(наличие
степенной функции с дробным показателем,
знаменатель которого есть четное число,
например, 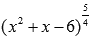 );Примеры
нахождения области определения степенной
функции...
);Примеры
нахождения области определения степенной
функции...
присутствие функции логарифма вида
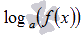 ,
например,
,
например,  или
или  ; Нахождение
области определения логарифмической
функции...
; Нахождение
области определения логарифмической
функции...
присутствие дробей вида
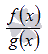 ,
например,
,
например, 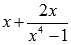 ; Нахождение
области определения дроби...
; Нахождение
области определения дроби...
присутствие функций тангенса вида
 и
котангенса вида
и
котангенса вида 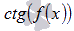 ,
например,
,
например, 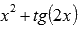 или
или  ; Примеры
нахождения области определения тангенса
и котангенса...
; Примеры
нахождения области определения тангенса
и котангенса...
присутствие функций арксинуса вида
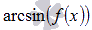 и
арккосинуса вида
и
арккосинуса вида  ,
например,
,
например, 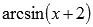 или
или 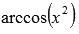 ; Примеры
нахождения области определения арксинуса
и арккосинуса...
; Примеры
нахождения области определения арксинуса
и арккосинуса...
присутствие показательно степенных функций вида
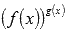 ,
например,
,
например, 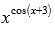 ; Нахождение
области определения показательно
степенной функции...
; Нахождение
области определения показательно
степенной функции...
присутствие любых комбинаций всех вышеперечисленных случаев, например,

Основные элементарные функции, их свойства и графики.
Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится.
В этой статье мы перечислим все основные элементарные функции, приведем их графики и дадим без вывода и доказательств свойства основных элементарных функций по схеме:
область определения функции;
поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);
проверка на четность и нечетность;
область значений функции;
промежутки возрастания и убывания, точки экстремума;
промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);
наклонные и горизонтальные асимптоты;
особые точки функций;
особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).
Как эти свойства были получены для каждой из основных элементарных функций можете ознакомиться в разделе полное исследование функции и построение графика.
Если же Вас интересует дифференцирование элементарных функций или интегрирование элементарных функций, то можете перейти к этим разделам теории.
Основными элементарными функциями являются: степенная функция с целым показателем степени, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
Степенная функция, ее график и свойства.

Показательная функция, свойства, график.
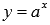 ,
где
,
где  ,
,  и
и 
Логарифмическая функция, ее свойства, графическая иллюстрация.
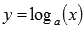 ,
где
,
и
,
где
,
и 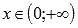
Свойства и графики тригонометрических функций.

Обратные тригонометрические функции (аркфункции), их свойства и графики.