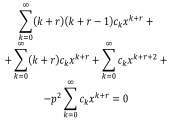Числ и Функц Ряды.
1. Понятие ряда: Пусть дана бесконечная последовательность (чисел, функций, и так далее)
величины a1 , a2 , ..., an , ... - элементы ряда, ak - общий элемент ряда. В результате вычисления значений этой функции при k=1, k=2, k=3, ... получаются все элементы ряда.
Определение 1.1. Если для произвольной последовательности построена бесконечная сумма вида (1), то говорят, определен ряд с элементами из заданной последовательности.
Классификация рядов. Ряды: числовые ряды и функциональные ряды. Числовые: ряды с положительными элементами и ряды с произвольными элементами (: Знакочередующиеся ряды (р. Лейбница)). Функциональные: степенные ряды (р. Тейлора) и тригонометрические ряды (р. Фурье).
Сходимость ряда. Основным понятием теории рядов является понятие сходимости числового ряда. Пусть дан ряд (1). Составим из его членов конечные суммы, называемые частичными суммами ряда:
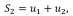
Если предел не существует (в том
числе и бесконечен), то ряд (1) называется
расходящимся.
Отрезок ряда:
Частичная сумма ряда:
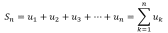
Остаток ряда:
Если ряд сходится, то остаток ряда – бесконечно малая последовательность.
Необходимый и достаточный признак сходимости ряда.
Необходимый признак сходимости ряда.
Свойства сходящихся рядов
1. Если ряды (6) и (7) сходятся, то их алгебраическая сумма – сходящийся ряд, сумма которого равна сумме исходных рядов
2. Произведение постоянного ряда на сходящийся - сходящийся ряд, сумма которого равна произведению постоянной на сумму ряда. Постоянная величина выносится за знак ряда:
3. Если из ряда (6) исключить или добавить конечное число элементов, то сходимость ряда не изменится: сходящийся ряд останется сходящимся, а расходящийся – расходящимся.
Действия над рядами
Постоянный ряд Сложение рядов Умножение рядов Деление рядов
2. Ряды с положительными элементами.
Элементы ряда (1) – неотрицательные числа. Последовательность частичных сумм ряда (1) – монотонно неубывающая последовательность, для сходимости которой достаточно потребовать ее ограниченности. Для ряда (1) так же справедлив критерий Коши.
Гармонический ряд.
Докажем его расходимость. Выполним группировку
оценка
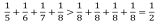
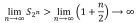Гармонический ряд расходится
Признак сравнения
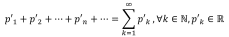
Пусть, начиная с некоторого номера, для числовых рядов с неотрицательными элементами (1) и (2) выполняются неравенства
Тогда справедливы следующие два утверждения
Теорема 2.1 (достаточный признак сравнения).
1. Если сходится ряд (2), то сходится и ряд (1).
2. Если расходится ряд (1), то расходится и ряд (2)
Теорема 2.2 (достаточный признак сравнения в предельной форме).
Если существует конечный, отличный от нуля предел выражения, то ряды (1) и (2) сходятся или расходятся одновременно
Докажем утверждение 1. первой теоремы
В достаточных признаках Коши и Даламбера в качестве ряда сравнения используется геометрическая прогрессия (сходящаяся или расходящаяся)
Достаточный признак сходимости Коши (радикальный)
Теорема 2.3. Если для ряда (1) существует конечный предел
Достаточный признак сходимости Даламбера
Теорема 2.4. Если для ряда (1) существует конечный предел
Достаточный признак сходимости Коши – Маклорена
3. Знакочередующиеся числовые ряды
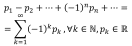Элементы ряда положительны. Знаки
чередуются.
Допустим, что элементы ряда (6) образуют монотонно убывающую бесконечно убывающую последовательность.
*
**
Понятие абсолютно и условно сходящегося ряда
Определение 3.1. Будем называть ряд (1) абсолютно сходящимся, если сходится ряд (2)
Теорема 3.1. Если сходится ряд (2), то сходится и ряд (1)
Доказательство. Воспользуемся критерием Коши. Требуется доказать, что выполняется
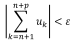
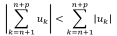
Сопоставляя неравенства, получаем искомое. Теорема доказана.
Определение 3.2. Ряд (1) называется условно сходящимся, если этот ряд сходится, в то время как соответствующий ряд из модулей (2) расходится.
Пример 3.2. условно сходящегося ряда
Решение. Воспользуемся формулой Тейлора
Для произвольного x
из сегмента [0;1]. Пусть x=1
4. Функциональные ряды.
Сходимость функционального ряда в точке и на множестве
5. Дифференцирование функционального ряда
Теорема 4.3. Пусть элементы ряда (1) - непрерывно дифференцируемые функции. А ряд составленный из производных элементов
сходится равномерно. Тогда сумма ряда (1) является дифференцируемой функцией, причем справедливо равенство
Интегрирование функционального ряда
Теорема 4.4. Пусть элементы ряда (1) – интегрируемые функции, а сам ряд сходится равномерно. Тогда сумма ряда так же является интегрируемой функцией, причем справедливо равенство
6. Степенные ряды.
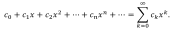
Определение 5.1. Ряд (1) называется степенным рядом.
1. Элементы ряда (1) – функции.
2. Область определения ряда (1) - ℝ.
3. Ряд (1) сходится в точке x=a, ряд (2) - в точке x=0.
Сходимость степенного ряда
Доказательство. Докажем пункт 1 теоремы. В силу условий теоремы сходится ряд
(*)
Следовательно, выполняется необходимый признак сходимости
(**)
Запишем исходный ряд (2) в виде
Рассмотрим ряд из абсолютных величин
(***)
В силу неравенств (**) имеем ряд, элементы которого не меньше элементов предыдущего ряда
(****)
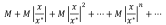Нахождение радиуса сходимости ряда. Должен выполняться достаточный признак сходимости ряда, например, Даламбера. Фиксируем x.
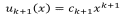
Аналогично признак Коши приводит к выражению
7. Разложение функции в степенной ряд
Поставим задачу. Сопоставить функции некоторый степенной ряд
Потребуем, чтобы значения функции и ряда, а также их производных совпадали в точке x=a
Продифференцируем функцию и ряд m раз. Получим
Ряд Тейлора для функции
Теорема 5.7 (единственность разложения). Если функция может быть разложена в степенной ряд, то это разложение единственно
Доказательство. Допустим противное
Продифференцируем м раз каждое из равенств. Положим x=a и вычтем одно из другого
Доказательство. Воспользуемся формулой Тейлора
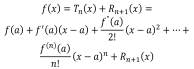
Запишем остаточный член
Многочлен Тейлора – частичная сумма ряда
Разложения в степенные ряды элементарных функций
Рассмотрим основные разложения элементарных функций в ряды Тейлора.
Тригонометрические функции
Показательные и гиперболические функции
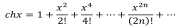
Логарифмические функции
Биномиальный ряд
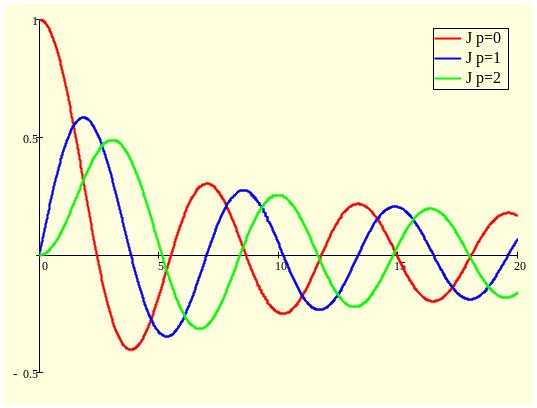
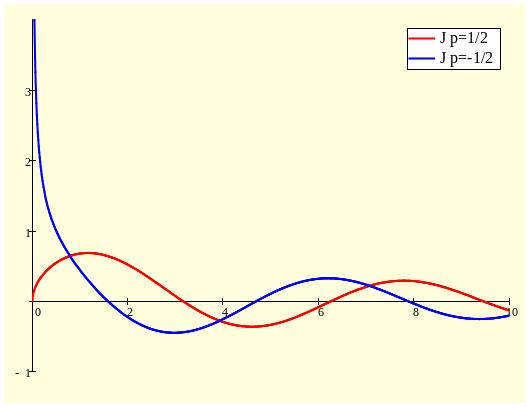
8. Уравнение и функция Бесселя
Рассмотрим однородное дифференциальное уравнение второго порядка.
Предполагая, что возможно дифференцирование под знаком ряда, вычислим производные.
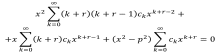
Подставим их в уравнение Бесселя
